[잭슨 전자기학] Ch 5.7, 5.8: 전류 분포가 만드는 힘과 토크; 자기장에 관한 경계조건

5. 7 Force and Torque on and Energy of a Localized Current Distribution in an External Magnetic Induction

학부과정에서도 봤듯, 전류밀도 J가 만드는 힘과 토크는 다음과 같다.

localized current distribution이 외부 장 B(x)에 놓이게 되면, 전류분포로 인해 자기장이 (천천히) 변하게 된다. 우선 위치 x에서의 자기장 B의 k번째 component는 다음과 같이 테일러 전개 가능하다. (당연히 k=x,y,z)

그럼 힘의 i번째 성분은 다음과 같다.

전에 유도했던 다음의 식을 이용하면,

를 얻을 수 있다. 따라서 다음의 결론을 얻는다. (m은 density가 아니라 총 자기모멘트임에 유의할것)

힘의 꼴로부터 퍼텐셜이 정의될 수 있음을 볼 수 있고, 다음과 같이 정의할 수 있다.

 

5.8 Macroscopic Equations, Boundary Conditions on B and H

물질 속 자기장을 논한다. 4장에서 bound charge를 논할 때( [잭슨 전자기학] Ch 4.5 , [잭슨 전자기학] Bound charge - 속박 전하 )와 사실상 거의 같은 이야기의 반복이다. 이 절에서 나온 얘기를 전부 포함하는 본격적인 논의를 6장에서 보게 될 것( [잭슨 전자기학] Ch 6.6 ) 이다.

 

average macroscopic magnetic moment(또는 magnetic moment density) M 을 다음과 같이 molecular magnetic moment m(소문자 m이지만 여기선 total magnetic moment가 아님)의 합으로 표현 가능하다.

 

이제 물질 내에서의 벡터퍼텐셜을 구하자. free current J(x')까지 포함하여 작은 부피 \( \delta V\) 안의 벡터퍼텐셜을 다음과 같이 쓸수 있고, 극한으로 보내고 적분하여 잘 알려진 macroscopic한 식을 얻을 수 있다.

(참고로 첫 식이 정전기학에서 봤던 식과도 매우 유사한 걸 볼 수 있다. [잭슨 전자기학] Ch 4.3 참고. 그래서 첫 식이 어디서 나왔냐 묻는다면 정전기학에서와 마찬가지로 localized distribution에 대한 벡터퍼텐셜 식을 multipole expansion해서 dipole 항까지만 남긴 식이라고 보아도 좋다. [잭슨 전자기학] Ch 4.1  참고.)

벡터 항등식을 이용해 식을 정리. 

이 작업.. electrostatics에서 스칼라 퍼텐셜 \( \Phi(x) \)에 대해서도 거의 유사하게 했던 작업이다.

그래서 마찬가지로 bound current density \( J_m \)과 surface bound current \(K_m\)을 정의해줄 수 있고.

no boundary(=boundary at infinity)를 가정하고 surface term이 1/r보다 빠르게 감소하여 0으로 간다 치면

와 같이 마지막 식(물질 속 암페어 법칙-정자기학 버전)을 얻을 수 있다. 여기서 도입한 H는 특별히 따로 이름이 붙어있진 않아 H field(그리피스에선 auxilary field라고 부르나 이 역시 뚜렷한 명칭은 아님)라고 부르거나 하는데, 이름이 없는 거에 비해 매우 중요하니 꼭 기억해야한다. 

첫 식에서 두번째 식으로 넘어간 방법은 직접 유도한게 아니라 첫 식에서 Jm이 effective하게 J이기 때문에 잘 알려진 \( \nabla \times B = \mu_0 J \)에 대입하여 얻어진 것이다.

따라서 다음과 같이 물질 내에서의 macroscopic한 식을 모두 얻을 수 있었다.

 

두 가지 더 언급할게 있다. 하나는 B와 H의 관계이고, 다른 하나는 경계조건이다.

1) B와 H의 관계

B와 H의 관계 (및 E와 D의 관계)를 Constitutive equation - Wikipedia 라고 부른다.  살펴보자.

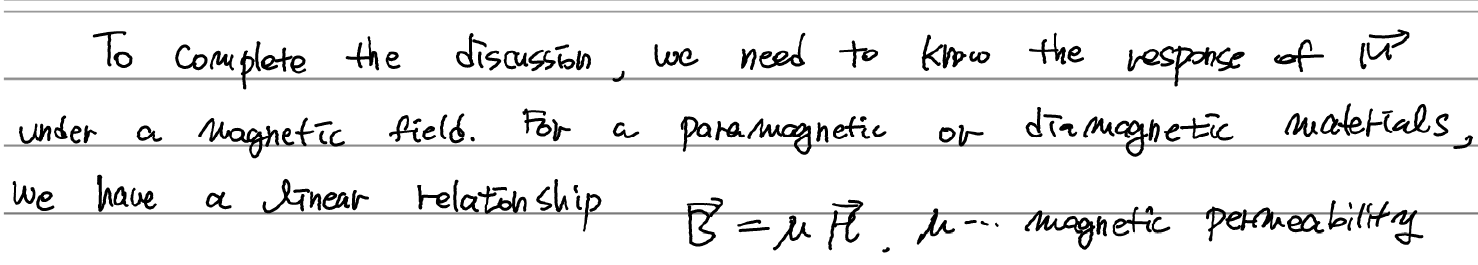
linear material의 경우, 예컨데 paramagnetic(상자성)이나 diamagnetic(반자성) 물질의 경우 \(B=\mu H\)가 성립. 정전기학에서 \( D= \epsilon E\)였던 것과 유사. 다음의 블로그 참고. Permeability(투자율) & Magne.. : 네이버블로그

그러나 Ferromagnetic(강자성) 물질의 경우는 다르다. B가 H에 대한 선형함수가 아니며, 게다가 히스테리시스가 나타난다.

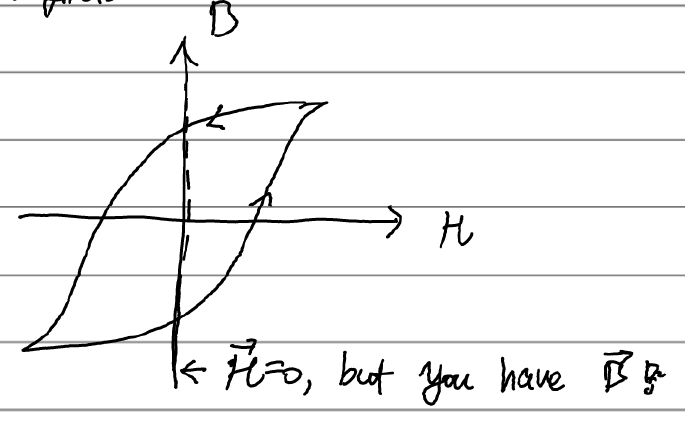
2) 경계조건

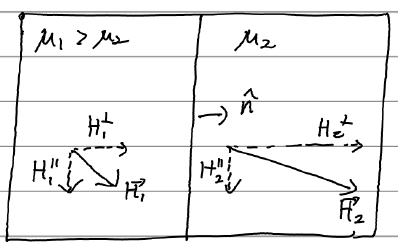
즉, 

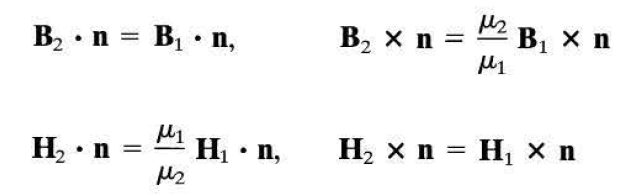
즉,

$$ B_1^\perp = B_2^\perp \Leftrightarrow \mu_1 H_1^\perp = \mu_2 H_2^\perp$$

$$ H_1^\parallel = H_2^\parallel \Leftrightarrow \frac{1}{\mu_1} B_1^\parallel = \frac{1}{\mu_2} B_2^\parallel$$

그래서 도체는 \(\mu\)가 무한대이기 때문에 도체 물질 표면에서 자기장은 항상 표면에 수직이 된다는 이야기.

 

정전기학과 경계조건 비교:

surface charge/current가 없는 상황일때, 정전기학에선 E_parallel이 서로 (무조건)같고 D_normal이 서로 같아야 하고( [잭슨 전자기학] Bound charge - 속박 전하 ), 정자기학에선 H_parallel이 같고 B_normal이 (무조건)같아야 한다( [잭슨 전자기학] Ch 5.7, 5.8: 전류 분포가 만드는 힘과 토크; 자기장에 관한 경계조건 ).  D_normal이랑 H_parallel은 각각 surface charge/ current가 존재시 그만큼 차이가 날 수 있다. 식은 두 링크 참고.