5.5 Vector Potential and Magnetic Induction for a Circular Current Loop

위와 같은 고리 도선을 따라 전류가 흐르고 있다. 전류밀도는 phi 성분만 존재하며, 다음과 같다.

(우변을 전체 부피에 대해 적분해주면 \(2 \pi a J \)가 나온다: J = (전체전류)/(둘레 길이)임과 부합)
전류밀도를 직교좌표계에서 쓰면 다음과 같다.
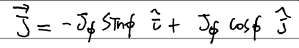
이제 벡터 퍼텐셜을 구할 건데, 계가 원통대칭성을 지니므로 xz 평면(phi' = 0) 에서의 퍼텐셜만 구해도 충분하다.
boundary가 없으면(=boundary가 infinity에 있으면) 벡터퍼텐셜은 다음과 같으므로

전류밀도 J와 평행하다. 즉, 우리가 구할 벡터퍼텐셜은 phi 성분만 존재한다. 이를 계산하면 다음과 같다.

(둘째 줄): 첫째줄에서 델타함수로 인해 \( \cos{\theta'} = 0, \sin{\theta'} = 1, r=a \)가 대입된 상황. 추가로 물결쳐진 \(\phi\) 가 0인 이유는 우리가 xz 평면상에서 벡터퍼텐셜을 구하는 중이기 때문.
(셋째 줄): 타원 적분을 이용하여 적분을 계산한 상황인데, 직접 해보려다간 끔찍한 치환적분 속에 갇혀 피를 볼 것이다. 그리 중요하지 않으니 눈으로 보기만 하고 넘어가도 된다.
구해진 결과를 특이하지만 다음과 같이 전개해보자.

그러고 나서 curl을 취하면 자기장을 얻을 수 있다. (특수함수를 어떻게든 전개를 해야 손으로 미분 가능하니까)

세 가지 흥미로운 영역이 존재하는데(theta<<1: 축 근처, r<<a : 원점 근처 , r>>a: 매우 멀리), 그 중 하나인 far-field, 즉 r>>a 영역에서의 자기장을 구해보면 다음과 같다.

5.6절에서 보게 되겠지만 dipole moment 꼴임은 우연이 아니다. (당연히 눈치채겠지만 이 경우도 multipole expansion이 존재한다)
벡터 퍼텐셜을 구하는 또다른 방법이 존재하여 소개한다. 3장에서 했듯 1/|x-x'|을 구면좌표계에서 전개하여 계산하는 것이다.

(둘째줄): \( \cos{\phi ' } \)를 \( e^{i \phi '} \)의 real part로 바꿔준 이유는 이것이 spherical harmonics의 m=1일 때 붙는 성분이기 때문. 이로써 spherical harmonics의 직교성을 이용할수 있게 된 것이다.

따라서 크로네터델타 \(\delta_{m1}\) 항이 나오게 될 것이고, 이것이 sum over m과 만나 m=1 항만 살아남게 되는 식으로 정리가 된다. 이것이 (셋째줄).
여기서 \( e^{i \phi '} \)이 sph. hmn.으로 처리가 된다면 그 때의 l값은 뭐여야하는지(=> 앞에 곱해져야하는 상수는 어떻게 구해야하는지), 또 왜 셋째줄 마지막의 Y_l1은 complex conjugate가 없는 것인지, 이런 부분에 대해 의구심이 들 것이다. 정상이다! 이를 따지기 위한 가장 확실하고도 편한(?) 방법은
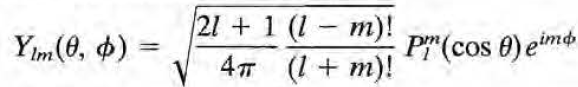
를 이용해 정리하는 것이다.
또 마지막의 식은 어떻게 나왔냐 하면, 마찬가지로 바로 위의 일반식으로부터 (+연관 르장드르 다항식의 일반식) 나온 것이다.
이를 다 합쳐 정리하여 쓰면,
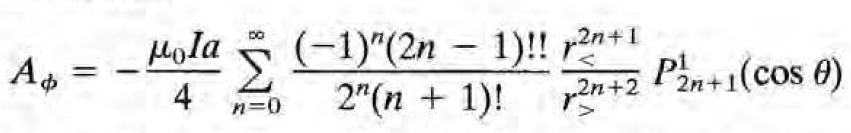
이 된다. (n=0일 때는 sum 바로 뒤 상수계수가 1이다. 그래서 분자에 (-1)!!이 들어가는 항은 생기지 않음)
이제 여기에 curl을 취하면 자기장을 구할 수 있다. 결과는 다음과 같다. (이 와중에 또 특이한 식을 써야하는 건 덤)

...이걸 직접 해볼 용자가 있을까?
다음과 같이 far-field를 구해보면 위에서 구했던 것과 일치하는 것을 확인할 수 있다. 추가로 원점 근처에서 z 방향으로의 자기장이 leading order로 나타난다고 한다. (정확히 z 방향이 아닌 이유는 원점이 아니라 원점 '근처'기 때문) 직관과도 부합하는 결과.

'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 5.7, 5.8: 전류 분포가 만드는 힘과 토크; 자기장에 관한 경계조건 (0) | 2024.11.30 |
|---|---|
| [잭슨 전자기학] Ch 5.6: 국소적 전류 분포가 만드는 자기장 (0) | 2024.11.30 |
| [잭슨 전자기학] Ch 5.1~5.4 : 정자기학(1) 비오-사바르 법칙, 앙페르 법칙, 벡터 퍼텐셜 (0) | 2024.11.05 |
| [잭슨 전자기학] Ch 4.4 Boundary-Value Problems with Dielectrics (0) | 2024.11.02 |
| [잭슨 전자기학] Bound charge - 속박 전하 (0) | 2024.10.13 |