( 작성일 : 2024-11-28 16:45)
6.6 Derivation of the Equations of Macroscopic Electromagnetism
미시적인 관점에서부터 거시적인 장에 대한 방정식인 맥스웰 방정식을 유도해보겠다, 바라보겠다. 이런 이야기를 하는 장이다. 과연 미시적인 세계에서도 우리의 맥스웰방정식이 동일할까.. 와 같은 생각도 동기가 될수 있겠다.
우선 다음의 생각으로부터 시작하자.

미시적인 세계의 전자기장은 점전하들이 다닥다닥 붙어있으므로 아주 조금만 위치와 시간이 변하더라도 매우 급변할 것이다.

이를 해결하기 위한 좋은 방법이 바로 '평균내기'이다. 어차피 macroscopic한 측정 과정 속에선 미시적관점에선 매우 큰 영역을 측정하게 될 것이므로 미시적인 요동은 전부 평균내져 사라지게 될 것이므로. 시간 또한 마찬가지.
미시적 관점과 거시적 관점을 구분하게 되는 스케일은 다음과 같다. 우선 거리의 경우, X-ray 회절 패턴이 고전장론으로 잘 설명되는 것으로부터 L0 ~ 10^-8m 정도가 둘을 구분하는 스케일이라고 볼 수 있다. 이로부터 시간의 스케일 또한 다음과 같이 구해진다.

즉 거리 L0 정도 안에서 평균을 내면 된다. 바꿔말하면, L0 이상의 거리부터는 '구분'되는 영역이다.
따라서 전자기장 E, B은 다음과 같이 미소전자기장 e,b를 평균내서 구할 수 있다.

test function f(x)는 거리 L0 안쪽의 영역을 고려해 평균을 내주고, 그 밖은 거시적으로는 다른 영역으로 구분하여 고려하지 않게 해주는 부드러운 함수이다. 특징만 만족하면 되기 때문에 예시로 써논 함수 외의 다른 함수도 가능하다. f를 그냥 곱해도 되는데, y축 기준 대칭적이므로 convolution으로 정의를 한 이유는 뒤에서 보게 될 것이다.
맥스웰 방정식에는 미분항들도 존재하므로 미분하는 경우에 대해서도 고려하면 다음과 같다.

천만다행히도 평균 기호 안에 미분 기호를 집어넣을 수가 있다. 따라서 다음을 쉽게 얻을 수 있게 되었다.

남은 두 식은 다음과 같이 소스 항이 들어가는 inhomogeneous eqn으로, 맥스웰 방정식을 얻기 위해선 소스에 관한 논의가 추가로 필요하다.


(오타: 마지막 식의 sum 밑의 기호가 j,n이 아니라 j(n)이어야 한다. n번째 분자의 j번째 전하들을 전부 sum한다는 것)
미시적으로, 전하분포는 점전하들의 집합이므로 델타함수의 sum으로 쓰이게 된다(양자역학적으론 전자의 waveftn이 공간 속에서 퍼져있지만, 우리가 지금하고자 하는 논의는 점전하를 이용한 철저한 고전적 논의임을 상기할 것). 매질의 분자들에 구속된 전하와 그렇지 않은 전하를 구분해서 써준 모습이다.
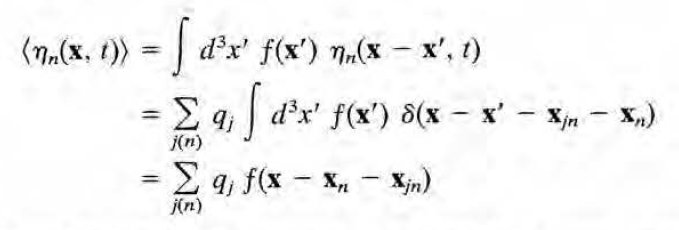
위 그림에도 나와있듯 여기서 x_n=x_n(t)는 원점으로부터 분자의 질량중심까지의 변위벡터고, x_jn=x_jn(t)는 분자의 질량중심으로부터 전하 q_j까지의 변위벡터이다. 이 둘의 합이 x_j=x_j(t)이다. 이 때 다음의 사실을 이용하여

테일러 전개를 하면 다음의 결과를 얻는다.
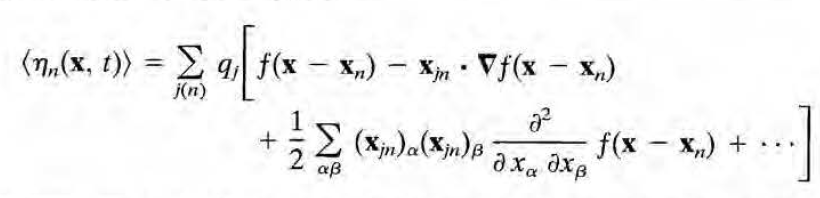
이렇게 튀어나온 각 항으로부터 다음과 같이 molecular multipole moment를 정의한다.
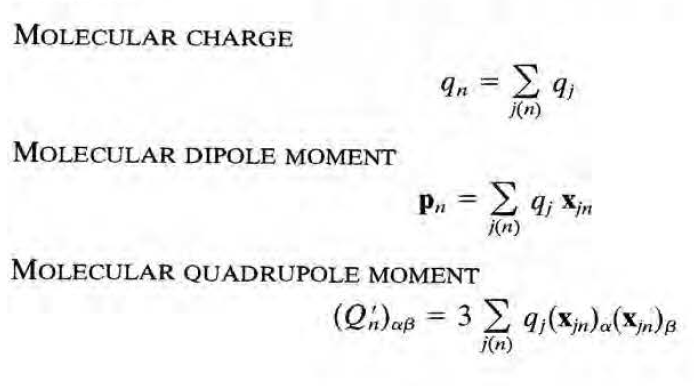
이 정의를 이용하여 식을 다시 써보면 다음과 같다.
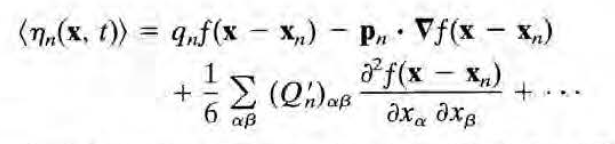
우변에서 f(x-xn)등이 적분 없이 존재하고 있을 수 있는 이유는 델타 함수와 함께 적분을 제거했기 때문이다. 따라서 델타함수와 적분을 다시 되돌려놓으면(= 평균 기호를 되돌려놓으면) 다음과 같은 과정을 거쳐
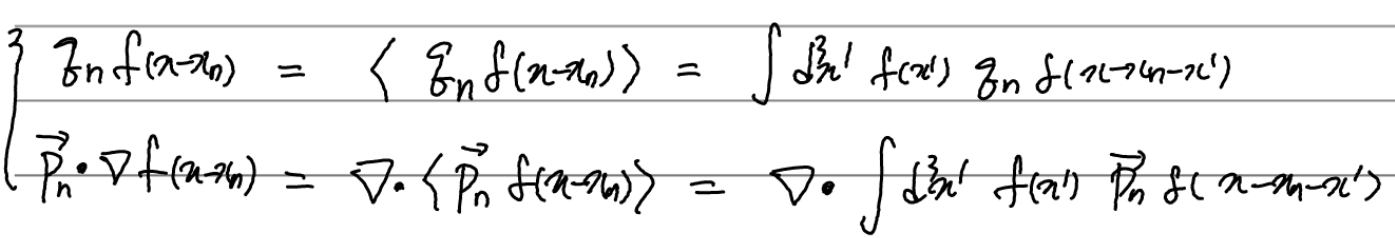
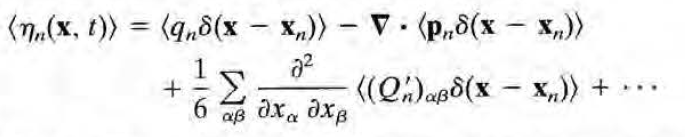
라는 식을 얻게 된다. 따라서 우리는 spatial averaging을 거치면 분자 내 여러 위치에 존재하는 점전하들을 그저 위치 x_n(=분자의 질량중심)에 존재하는 multipole들의 합으로 볼 수 있음을 알게 되었다.

이제 free charge까지 포함하여 논의를 마무리 짓자.
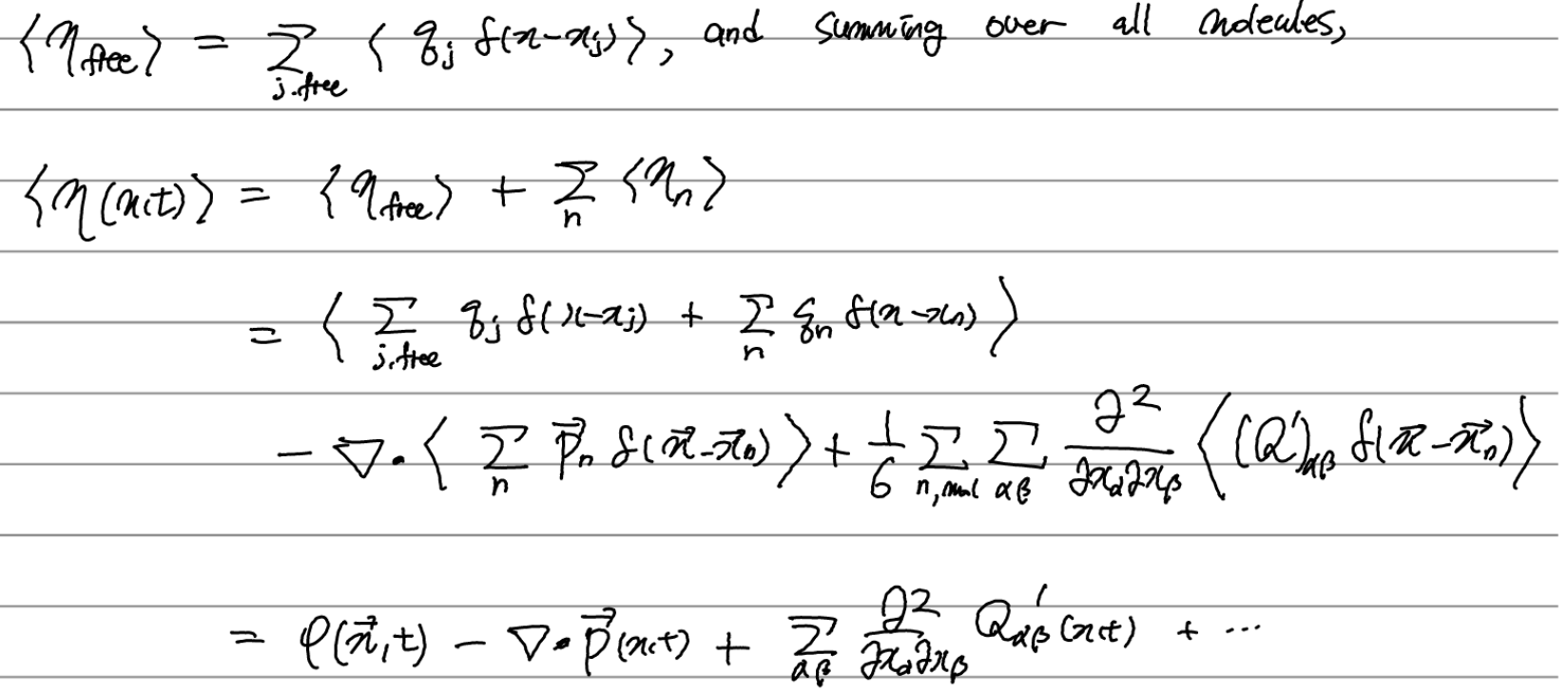
따라서 macroscopic한 물리량들은 다음과 같이 정의될 수 있다(혹은 미시적 관점과 이러한 관계를 맺는다). 위에서 정의된 molecular multipole moment들(subscript로 n이 붙은 것들)이 쓰인 것을 볼 수 있다.
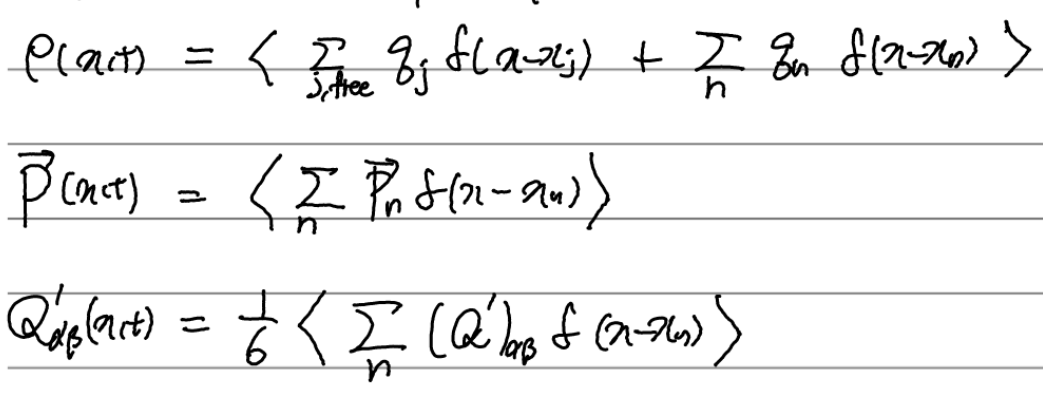
이제 아직 유도하지 않은 두 맥스웰 방정식 중 하나를 유도할 수 있게 되었다.

(마지막 D_a 식에서 세번째 항은 아인슈타인 노테이션으로 beta에 대한 sum이 포함되어야 한다)
즉 우리가 이전 장에서 다루었던 linear dielectric이 아니라면
마지막 맥스웰 방정식을 유도하기 위해선 미시적 관점의 전류에 대한 논의를 해야한다. 우선 microscopic current density는 다음과 같이 쓰인다.
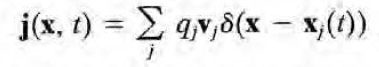
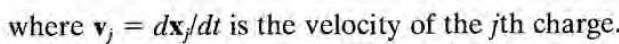
평균내면 다음과 같다. 이때 index는 이전과 동일한 의미이다. 가령 vn은 분자의 질량중심의 속도, vjn은 점전하의 상대속도이다.

테일러 전개를 하고 이를 위에서 정의했던 macroscopic한 물리량들로 써보면 다음과 같다. (문제 6.7이 이를 유도해보라는 문제다. 그런데 해보면 그리 간단하지 않다. 오히려 엄청...엄청 복잡하다... 심지어 우변의 마지막 항(세번째 줄)은 좌변의 2계미분항을 주지 못한다. 좌변의 2계미분항을 완성하려면 D-e0E에서 나오는 electric octopole 뿐만 아니라 우변에 magnetic quadrupole에 관한 항이 추가로 존재해야한다(마치 1계미분항에 대해선 세번째 항이 존재하듯).)

여기서 J와 M은 다음과 같이 정의된 물리량이다.
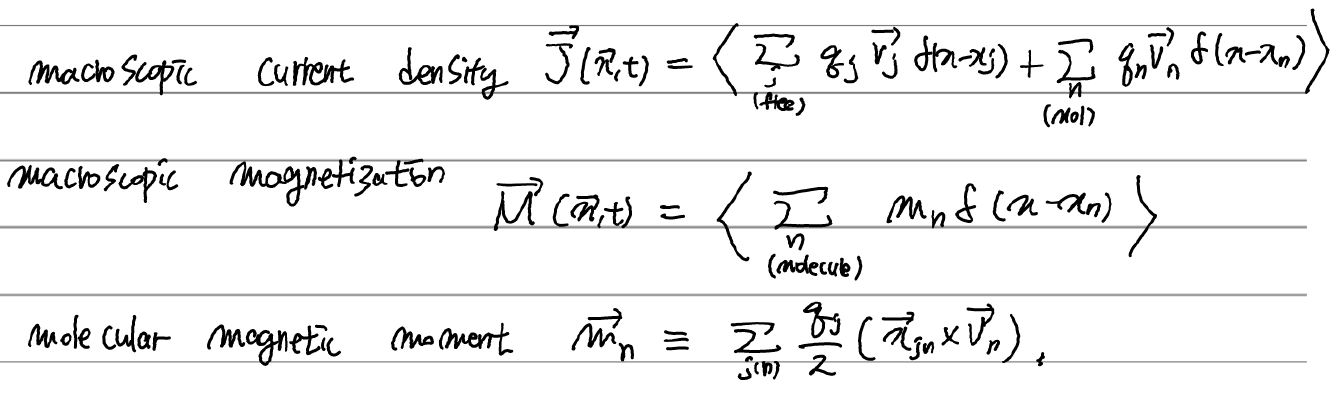
위 식은 벡터의

이제 다음의 유도과정을 따라가보자.

B=<b>임을 상기. macroscopically, v_n=0. 따라서 이렇게 맥스웰 방정식의 마지막 식이 유도되었다!
v_n이 0이 아니라 v(그치만 여전히 매우 작은값)이라고 했을 때 어떤 영향이 있는지 보도록 하자. 최종 결과는 다음과 같다. (뭔가 바로 위에서와 모순되는 것만 같다... H=<b>/mu0 -M = B/mu0 -M으로 정의되었는데 이와 바로 다른 식이 되었으니까. 아래 식을 H의 진짜 정의라고 생각하고 보면 위의 식 또한 유도될 수 있고(맥스웰 방정식이 제대로 나오고) 문제되지 않는다)
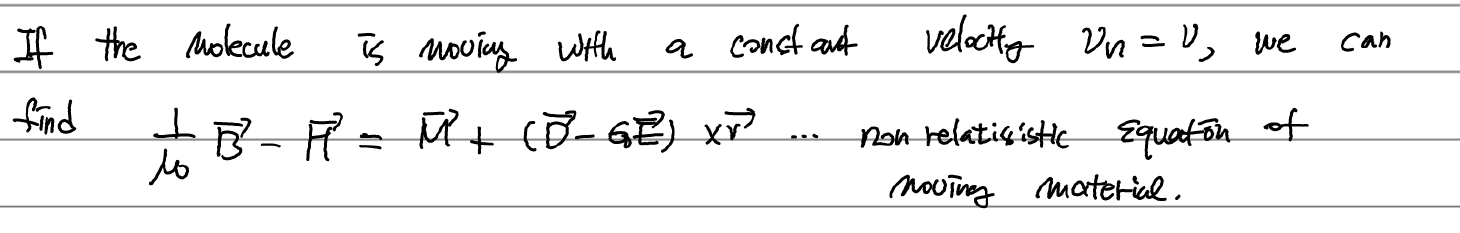
위 식을 유도하기에 앞서 다음의 lemma를 잠깐 보고가자.
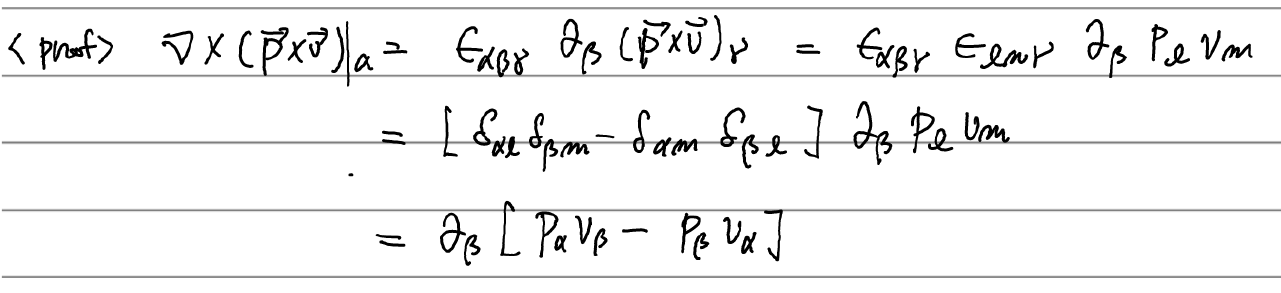
이제 유도해보자.

(첫 식):
네번째 항에서 바로 위의 lemma 사용
(셋째 식): 둘째 식에서 curl을 전부 벗김. 우변 뒷항의 평균을 계산한 결과에서 P는 꽤 위에서 정의한 macroscopic polarization.
(넷째 식): P를 D-e0E로 돌려놓았다. 사실 둘째 식에 quadratic tern도 존재하기에 셋째 식은 다소 부정확한데, 넷째 식의 D는 quadratic term을 포함하기에 둘째식과 마찬가지로 정확한 식이 되었다.
두 가지 언급할 것이 있다.
(1) spatial average of microscopic quantities
우선 우리의 '평균'은 convolution임을 기억할 필요가 있다. convolution의 특징은, 푸리에 변환시 곱으로 바뀐다는 것이다.

(여기서 푸리에변환은 time->freq domain이 아니라 position->momentum or wavenumber domain임에 유의)
우리가 썼던 test function f(x)는 주어진 성질을 만족하기만 하면 어떤 것이든 상관없었는데, 논의의 편의를 위해 가우시안 함수를 택하자. 가우시안 함수는 푸리에변환 후에도 가우시안 함수라는 특징이 있다. 따라서 '평균'내어지는 함수가 무엇이 되었든 간에 푸리에변환된 wavenum domain에선 큰 k값에서 항상 가우시안함수와 곱해져 suppression된다. 파장으로 따지면, 작은 거리에 대해 suppression이 이뤄진다는 것이다. 따라서 convolution이 우리의 '평균내기'와 이렇게 연결될 수 있는 것이다. 다음을 참고.

돌아와서, 푸리에 변환과 convolution의 특징을 이용하여 기존의 식을 재유도 해보자.

(단순히 푸리에변환과 테일러전개를 이용한 것)

(둘째줄 첫항): q_n 튀어나오고 f(k)가 푸리에변환되어 f(x-xn)이 됨
이렇게 재유도를 마친다.
(2) quadrapole moment

우리의 molecular quadrapole moment(Q')는 일반적인 quadrapole moment(Q)와 달리 traceless가 아니다. 이걸 두고 missing factor라 한것. 그래서 일반적인 Q 식에 들어있는 것처럼 크로네커델타가 포함된 항을 빼주어 traceless가 되도록 맞춰주었다.

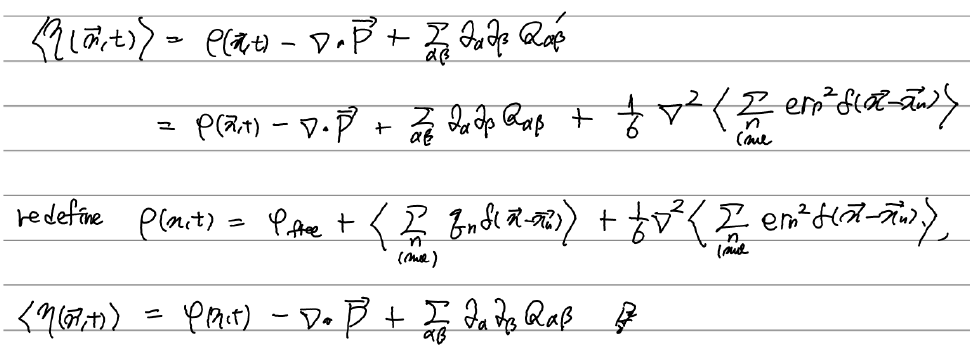
쭉 따라 읽어보면 된다. rho의 정의를 적절히 업데이트하면(마지막의 세번째 항을 추가하면) quadrapole moment를 traceless로 만들수 있다는 이야기다. 잭슨 257쪽 하단부터 뭔가 더 논의가 있는데 잘 이해가 안돼서 패스했다. 다만 식에 관해 하나 메모해둘만한게 있어서 따로 포스팅을 발행. 평면파와 spherical sinc function(sin(kr)/kr) 간의 관계
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화 (0) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 6.7 포인팅 정리: 전자기장과 전하 계의 에너지 보존정리 (0) | 2024.12.06 |
| [잭슨 전자기학] ch 6.5: 움직이는 점전하가 만드는 전기장과 자기장 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.4 : 로렌츠 게이지 하의 맥스웰 방정식을 풀기 위한 시간 의존적 그린 함수 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.1, 6.2, 6.3: 맥스웰 방정식, 게이지 (0) | 2024.12.06 |