정자기학(Magnetostatics)을 다루는 챕터다. 학부때랑 크게 달라지는 내용은 없다.
이전 챕터들에서는 그린함수를 도입하여 정전기학 문제들을 풀었다면, 정자기학에서는 그런 새로운 방법도 등장하지 않는다. 특수함수들과 함께 더 복잡한 상황들에 대해 더 복잡한 계산들을 행할 뿐이다..
(정자기학에서 그린함수가 사용되지 않는 이유: 정전기학에서 그린함수를 사용했던 이유는 퍼텐셜이 스칼라였고, 그린항등식이 스칼라장에 대한 식이였기 때문이다. 고로 정자기학에서도 그린함수를 사용하려면 벡터장에 대한 그린항등식과 같은 것이 존재해야 하고 이로부터 그린함수 포멀리즘을 구성하여야 하는데, 복잡하여 거의 쓰이지 않는다. 궁금하다면 (ENZCon 2016 Proceedings.pdf \342\200\224 proceedings_cover) 등의 자료 참고.)
5.1 Introduction
생략
5.2
이 절의 핵심적인 내용은 세 가지.
(1) 비오-사바르 법칙(Biot-Savart law) (1820)

$$ d\vec{B} = \kappa I \frac{d\vec{l} \times \vec{x}}{|\vec{x}|^3} , \quad \kappa = \frac{\mu_0}{4\pi} = 10^{-7} N/A^2 $$
방향은 오른나사 법칙으로 쉽게 따질 수 있다.

(2) 앙페르의 실험 (1825)

닫힌 고리 형태의 전선 간의 힘에 관한 공식을 실험 데이터 분석을 통해 얻었다.
$$ \vec{F}_{12} = \frac{\mu_0}{4\pi} I_1 I_2 \oint \oint \frac{d\vec{l}_1 \times (d \vec{l}_2 \times \vec{x}_{12})}{|\vec{x}_{12}|^3} $$
여기서

임을 이용하면

와 같이 정리 가능하다.
(3)

5.3

이로부터 \( \nabla \cdot \vec{B} = 0\) 를 유도할 수 있다.
유도과정:

따라서 curl의 divergence가 0으로부터 유도됨.
또한, steady current에 대해

가 성립한다.
유도과정:

위의 자기장의 curl에 대한 식의 적분형을 앙페르 법칙(Ampere's Law)이라고 한다.

정전기학(electrostatics)과 비교하면
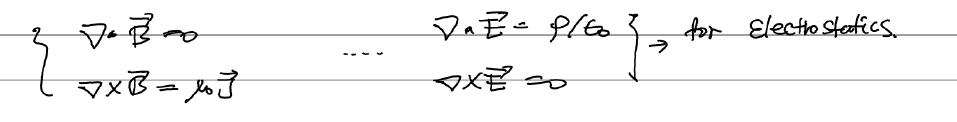
5.4 vector potential
정전기학에서 전기장을 어떤 다른 함수(scalar potential)의 미분 형태로, \( E = - \nabla \cdot \Phi \)로 썼던 것처럼, 자기장도 어떤 다른 함수의 미분 형태로 써보도록 하자. 다만 이번엔 curl을 이용해 \( B = \nabla \times A \)로 쓰자. 이 A를 vector potential이라고 한다.

마지막의 psi는 arbitrary scalar field. (electrostatics에서의 scalar potential에서도 유사한 상황을 봤던 기억이 있을 것)
이를 적절히 선택함으로써
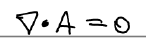
를 만족시키도록 할 수 있으며, 이 조건을 Coulomb gauge라고 한다. 굳이 이 조건을 만족시켜야만 하는 이유는 없고, 단지 특정 상황의 경우 이러한 조건을 주었을 때 문제가 더 쉽게 풀리기 때문이다. 이 조건이 유용한 이유는

과 같은 이유로 푸아송 방정식으로 바꿀 수 있기 때문이다. 벡터장의 라플라시안은 직교좌표계에서 단순히 다음과 같이 쓰인다.
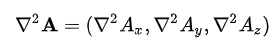
다른 좌표계에서 어떻게 쓰이는지 궁금하다면 Del in cylindrical and spherical coordinates - Wikipedia 참고.
unbound space에서 이를 풀면(사실 새로 다시 풀어도 되지만 5.4절 첫 사진의 식으로부터도 쉽게 유도 가능)

이 나온다.
왜 psi=0 (for all space)이냐 하면,

Coulomb gauge 외에도 다른 gauge 조건들도 많이 있다. Gauge fixing - Wikipedia 참고.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 5.6: 국소적 전류 분포가 만드는 자기장 (0) | 2024.11.30 |
|---|---|
| [잭슨 전자기학] Ch 5.5: 정자기학(2) - 고리 전류가 만드는 자기장과 벡터퍼텐셜 (0) | 2024.11.13 |
| [잭슨 전자기학] Ch 4.4 Boundary-Value Problems with Dielectrics (0) | 2024.11.02 |
| [잭슨 전자기학] Bound charge - 속박 전하 (0) | 2024.10.13 |
| [잭슨 전자기학] Ch 4.6 (0) | 2024.10.13 |