사실 ch3 내용을 작성하면서 공부는 많이 됐는데 효율이 너무 떨어져서 살짝 고민중이다. 그래도 4장 내용은 학부 떄 대충대충 했어서 4장까진 전체 내용을 쭉 풀어쓰는걸로..
4.1 Multipole expansion
$$ \Phi(\vec{x}) = \frac{1}{4 \pi \epsilon_0} \int \frac{\rho(\vec{x}')}{|\vec{x}-\vec{x}'|} d^3 x' $$
전하밀도 \(\rho\)가 localized charge distribution일 경우에 대해 알아보자. 간단히, 원점을 중심으로 하는 반지름 R의 구 안에서만 \(\rho \neq 0\)인 경우를 가정하자. 그럼 구 밖에서는 \(r_{\lt} = r' , r_{\gt} = r\)이므로 퍼텐셜을 다음과 같이 정리할 수 있다.
$$ \Phi(\vec{x}) = \frac{1}{\epsilon_0}\sum_{l,m} \frac{1}{2l+1} \left[ \int Y^*_{lm} (\theta', \phi') r'^l \rho(\vec{x}') d^3 x' \right] \frac{Y_{lm} (\theta, \phi)}{r^{l+1}} $$
그럼
$$ \Phi(\vec{x}) = \frac{1}{4 \pi \epsilon_0}\sum_{l=0}^{\infty} \sum_{m=-l}^{l} \frac{4\pi}{2l+1} q_{lm} \frac{Y_{lm} (\theta, \phi)}{r^{l+1}} $$
$$\text{where } q_{lm} := \int Y^*_{lm} (\theta', \phi') r'^l \rho(\vec{x}') d^3 x'$$
로 정리할 수 있고, 이렇게 정의한 \(q_{lm}\)을 (spherical) multipole moments라고 한다.
반면 다른 방식의 전개도 가능하다. Multipole expansion - Wikipedia 에서 소개된 것처럼, 1/|x-x'|을 바로 테일러 전개하는 것이다. (결과는 조금 밑에서)
그리고 이로부터 multipole moment를 정의하면, 위에서 정의한 spherical multipole moment와는 다른 식이 나오게 되는데, 이를 cartesian multipole moment라고 한다. 그래서 그냥 multipole moment라고 하면 맥락에 따라 둘 중 어느것도 될 수 있으나, cartesian multipole moment를 지칭할 때가 더 많다.
cartesian multipole moment의 예시부터 소개를 하자면,
- total charge
$$q = \int \rho(\vec{x}') d^3x'$$
- dipole moment
$$ \vec{p} = \int \vec{x}' rho(\vec{x}') d^3 x' $$
(참고로 dipole moment의 방향은 -전하에서 +전하 방향으로 향함 => dipole이 만드는 전기장의 방향은 p와 반대방향. 밑에 나오는 퍼텐셜 식을 미분해 구한 전기장을 봐도 확인가능)
- quadrupole moment
$$ Q_{ij} = \int(3x'_i x'_j - r'^2 \delta_{ij}) \rho(\vec{x}') d^3 x' $$
rank-2 텐서로, traceless 3x3 행렬로 쓸 수 있다.
이렇게 정의된 cartesian multipole moment를 이용하여 전개한 결과는 다음과 같다.

참고로 이 식의 다음 항(octupole)부터는 쓰기 급격히 어려워진다고 한다고 잭슨엔 써있는데, rank-3 tensor여서 그런건가 싶어서 찾아봤더니 유도는 복잡해도 최종꼴은 그리 복잡하진 않은 느낌이다. potential - Electric octupole moment in cartesian coordinates - Physics Stack Exchange 와 Quadrupole moment.pdf (physicspages.com) 참고.
다시 spherical multipole moment로 돌아와서, 구체적인 예시를 소개하자면 다음과 같다.

각 식의 두번째 등호 이후에 나오는 q, p, Q가 바로 cartesian multipole moment이다. 이 때문에 cartesian multipole moment를 잠시 미리 소개하였다.
spherical multipole moment의 성질로 한가지 언급되는 것은
$$ q_{l,-m} = (-1)^m q^*_{lm} $$
으로, spherical harmonics의 성질로부터 그대로 기원하였다.
퍼텐셜을 구했으니 전기장도 구해보자.

그리고 여기서 \(\partial Y_{lm} /\partial \theta\)와 \(Y_{lm}/ sin \theta \)는 다른 \(Y_{lm}\)들의 선형 결합으로 쓸 수 있다. 9장에서 등장할 vector spherical harmonics라는 걸 이용하면 된다는데, 그냥 양자역학에서 |l,m> state에 ladder operator 취하는 방식과 별반 다르지 않다. 식 (9.101)~(9.104) 부분에 나오는,
$$ \vec{L} = \frac{1}{i} (\vec{r} \times \nabla ) $$
$$ \begin{cases} L_+& = L_x + iL_y & = e^{i\phi} (\frac{\partial}{\partial \theta} + i \cot{ \theta} \frac{\partial}{\partial \phi} ) \\ L_- & = L_x - iL_y & = e^{-i\phi} (-\frac{\partial}{\partial \theta} + i\cot{\theta} \frac{\partial}{\partial \phi} ) \\ L_z & = -i \frac{\partial}{\partial \phi} \end{cases} $$
$$ \begin{cases} L_+ Y_{lm}& = \sqrt{(l-m)(l+m+1)}Y_{l,m+1} \\ L_- Y_{lm}& = \sqrt{(l+m)(l-m+1)}Y_{l,m-1} \\ L_z Y_{lm}& = m Y_{lm} \end{cases} $$
이들을 조합하면 된다. 많이 더럽긴 하다. 가령 \(\partial Y_{lm} /\partial \theta\)의 경우는 \( (e^{-i \phi} L_+ Y_{lm} - e^{i\phi} L_- Y_{lm})/2 \)로 구할 수 있다.
dipole(l=1)에 대해서만 전기장을 구체적으로 구해보면

이를 정리하면

라고 한다.
두 가지 중요하게 언급할 게 있다.


좌측과 같은 표현은 직교좌표계에서의 multipole moment의 표현이고, 우측과 같은 표현은 구면좌표계에서의 multipole moment의 표현이다. 여기서 중요한 건, 직교좌표계에서의 표현은 (l+1)(l+2)/2개(예를 들어 l=1일 때의 차원은 3인데, 이는 \( \bf{p} \)의 차원 3과 같다. 또, quadrupole은 i,j=1,2,3 에 traceless이므로 3*3-3=6=(2+1)(2+2)/2이다.), 구면좌표계에서의 표현은 (2l+1)개 ( \(-l \leq m \leq l \)로, 둘이 같지가 않다는 점이다(l이 1보다 클 때는 직교좌표계에서가 항상 값이 크다). 그러나 이는 모순이 아니다. 두 multipole moment는 회전변환에 대해 다른 특징을 가지기 때문이다 - 그리고 이는 직교좌표계 버전은 reducible, 구면좌표계 버전은 irreducible이라는 차이로 이어진다(수식적 논리로는 전후가 바뀌는게 맞지만). 문제 4.3 참고. 관련하여 electromagnetism - How to prove that spherical and Cartesian $l$th multipole moments have the same number of independent components? - Physics Stack Exchange 도 참고.
두번째로 언급할 중요할 사항은 구면좌표계에서의 multipole moment(=q_lm)가 원점의 위치좌표에 의존할 수도, 안 할 수도 있다는 것이다. 정확히는 주어진 전하 분포의 0이 아닌 다중극 모멘트 중 가장 낮은 차수의 다중극 모멘트는 원점의 위치좌표에 독립이나, 그 이상에선 일반적으로 의존하게 된다. 예를 들어 rho가 dipole+quadrupole+.. 형태면 monopole moment(=total charge)은 0, dipole moment부터는 0이 아닌데, dipole moment가 0이 아닌 가장 낮은 차수의 다중극 모멘트이므로 원점에 독립이나 quadrupole moment부터는 일반적으로 원점에 의존할 수 있게 된다는 것. 문제 4.4를 참고. 참고로 문제 4.4의 (2l+1) moments of multipole이라는건 order l의 multipole의 경우 구면좌표계에서의 multipole moment가 2l+1개이기 때문.
다음으로 이런 계산을 해보자. localized charge distribution rho(x)에 의해 전 공간에 전기장이 만들어지는 상황을 생각하고, 원점을 중심으로 하는 구 안의 전기장의 부피적분을 해보자.
$$\begin{eqnarray}
\int_{r<R} \mathbf{E}(\mathbf{x}) d^3 x &=& -\int_{r<R} \nabla \Phi d^3 x = -\int_{r=R} R^2 d\Omega \Phi(\mathbf{x}) \mathbf{n} \nonumber \\
&=& - \frac{R^2}{4 \pi \epsilon_0 } \int d^3 x' \rho (\mathbf{x'}) \int_{r=R} \frac{\mathbf{n}}{\left| \mathbf{x}- \mathbf{x'} \right|} \nonumber \\
\end{eqnarray}$$
where \( \bf{n} \) is the outwardly directed normal ( \( \mathbf{n} = \mathbf{x}/R \) )
두번째 등호는 스토크스 정리나 발산정리의 결과가 아니라, gradient를 고려해 직접 계산한 결과. 잭슨 교재 극초반 Theorems from Vector Calculus에 있는 두번째 공식을 사용한 것으로 생각해도 됨.
이제 여기에
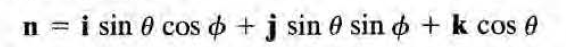
을 대입하여 정리하면 됨. 정리를 편하게 하는 방법이 있는데 바로 n의 각 component( sintheta cos phi 등)를 spherical harmonics로 정리(해보면 l=1일때 식만 쓰인다)하고, 위 식에 다음의 식도 대입한 뒤 spherical harmonics의 orthogonality를 이용하는 것이다.
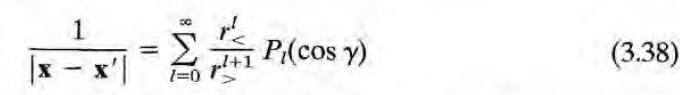
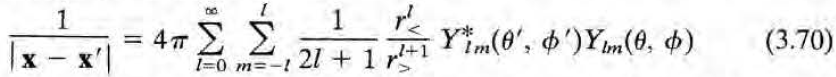
그러면 다음처럼 정리가 된다. (l=1 term만 살아남을 것이므로 P_1(cos r) = cos r로부터 이리 될 것이다)
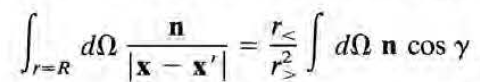
이제 여기에
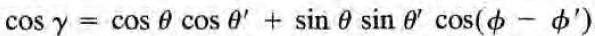
를 대입하여 적분을 수행하면 위 적분은
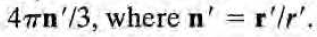
가 나온다. 구체적으로는 아래 더보기 참고.
따라서
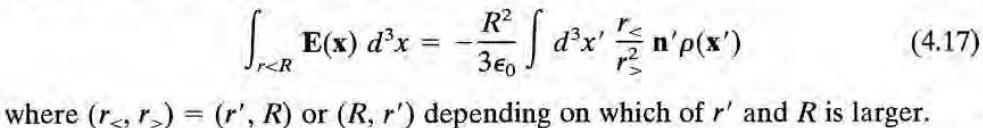
가 나온다.
이제 다음의 두가지 케이스를 생각해보자.
(1) rho가 전부 R 안에 있을 때 : \( r_{<} = r' \) and \( r_{>} = R\)
$$ \int_{r<R} \mathbf{E} (\mathbf{x}) d^3x = - \frac{1}{3\epsilon_0} \int d^3x' r' \mathbf{n'} \rho(\mathbf{x'}) = - \frac{1}{3\epsilon_0} \int d^3x' \mathbf{r'} \rho(\mathbf{x'}) = -\frac{\mathbf{p}}{3 \epsilon_0} = - \frac{4 \pi R^3}{3} \frac{\mathbf{P}}{3 \epsilon_0} $$
즉 R 안에 rho가 전부 있기만 한다면 이 적분 결과는 R에 의존하지 않는다.
(2) rho가 전부 R 밖에 있을 때 : \( r_{<} = R\) and \( r_{>} = r'\)
$$\begin{eqnarray} \int_{r<R} \mathbf{E} (\mathbf{x}) d^3x &=& - \frac{R^2}{3\epsilon_0} \int d^3x' \frac{ R \mathbf{n'}}{r'^2} \rho(\mathbf{x'}) = - \frac{R^3}{3\epsilon_0} \int d^3x' \frac{ \rho(\mathbf{x'}) }{r'^2} \mathbf{n'} \\&=& - \frac{R^3}{3\epsilon_0} (4 \pi \epsilon_0) \frac{1}{ 4 \pi \epsilon_0 } \int d^3x' \frac{ \rho(\mathbf{x'}) }{r'^2} \mathbf{n'} =\frac{4\pi}{3} R^3 \mathbf{E}(\mathbf{x}=\mathbf{0}) \\ \end{eqnarray}$$
즉, 내부에 전하분포가 없을 때 구 내부 전기장의 평균값은 구의 중심에서의 전기장의 값과 같다!(양변을 4pir^3/3으로 나눠보라) 묘하게 문제 1.10과 닮은 구석이 있는 것 같기도(전기장을 전위로, 내부를 표면으로 바꾼 버전).
이제 (1)을 이용하여 위에서 구했던 dipole이 만드는 전기장 식을 수정해보자.

dipole이 존재하는 위치를 아주 작은 구로 둘러싸고, 그 구 내부에서의 전기장을 (1)로 표현하고, 구의 부피를 0으로 보내보면 다음과 같이 디랙델타 항이 추가되어야 한다. (부피에 대해 적분한 값이 상수인데 부피가 0이려면 적분인자가 디랙델타여야.)
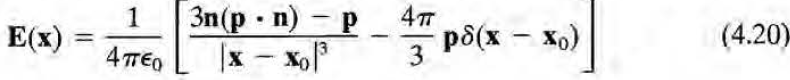
이는 후에 나올 localized circulating current source가 만드는 자기장 공식과도 닮았다.
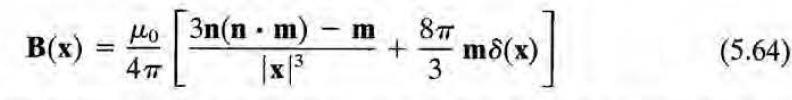
디랙델타 항은 finite distribution of charge and current를 다루는데 있어 필수적이다.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 4.3 (0) | 2024.10.12 |
|---|---|
| [잭슨 전자기학] Ch 4.2 (0) | 2024.10.11 |
| [잭슨 전자기학] Ch3 - (4/4) (0) | 2024.10.05 |
| [잭슨 전자기학] Ch3 - (3/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
