[잭슨 전자기학] Ch 5.15, 5.16 : 패러데이의 법칙, 자기장의 에너지

5.14 Numerical Methods/or Two-Dimensional Magnetic Fields 절은 전산시뮬레이션 공부할 거 아니면 필요 없고 그마저도 잭슨으로 공부할 필요없음. 생략

 

5.15 Faraday's Law of Induction

이제 time-dependent한 상황을 처음으로 다루게 된다. 패러데이의 실험은 설명 생략. 결과로 얻은 식은 다음과 같다.

C는 전선 뿐만 아니라 공간상에서 임의로 잡은 폐곡선이어도 됨.

C를 v의 속도로 움직이면?에 관한 이야기.

참고로 처음의 전미분식은 material derivative라고 부르기도 함. 이를 앞선 식에 대입해주면 다음을 얻음.

첫식의 두번째 항은 스토크스 정리를 쓴것. 두번째 식으로 넘어갈때 B와 v 순서가 바뀐 것을 확인하기.

이 때 E'의 프라임은 C가 정지된 것으로 보이는 관찰자의 프레임에서의 전기장임을 말하기 위해 붙은 것이다. 맨처음 식은 C가 정지해있을 때 성립하는 법칙이기 때문이다.

 

E는 C가 v의 속도로 움직이는 것으로 보이는, 처음의 프레임에서의 전기장이다. 프라임이 있을 때와 없을 때의 상황을 헷갈리지 말것. 

지금 우리는 전기장의 갈릴레이 변환을 유도한 것과도 같다. 즉 v<<c일 때6 무언가 움직이는 상황의 문제를 이 변환을 통해 멈춰놓고 생각할 수 있다(예: 문제 6.4).

 

물론 갈릴레이 변환은 비상대론적이므로, 일반적이진 못하다. 특수상대론적 변환, 즉 로렌츠 변환을 적용해서 얻은 일반적인 식은 다음과 같다.

아무튼, 결과를 differential form으로 적으면 다음의 식, 패러데이 법칙을 얻는다. 이는 곧 맥스웰 방정식의 세번째 식이 된다.

 

5.16 Energy in the Magnetic Field

 

고등학교에서도 배우지만 자기장은 일을 못한다. 항상 이동방향의 수직 방향으로 작용하기 때문.

그럼에도 우리가 자기장의 에너지를 얘기할 수 있는 이유는 패러데이의 법칙에 따라, 자기장의 시간에 따른 변화가 전기장을 유도할 수 있고 전기장은 일을 할 수 있기 때문이다.

전류 I가 흐르는 닫힌 회로를 생각하자. 이를 통과하는 자기장 B(t)가 시간에 따라 변하면, electromotive force가 작용하게 되고, 전류를 I로 유지해주기 위해선 emf에 저항하기 위한 일을 해줘야만 한다. 이 일을 측정함으로써 다음의 법칙을 얻어내었다.

 

이제 위 상황을 일반화해 논의해보자. Steady current J를 생각하자. 자기장이 변할시 emf에 의해 전류도 변하게 될텐데, 이를 방지하기 위해 매우 짧은 시간 간격을 생각하자. 또 전체 circuit을 매우 작은 면적의 elemental circuit으로 분해하여 생각하자. elemental circuit에서 전류가 흐르는 면적(cross section)을 \(\Delta \sigma\)로 놓자.

 

 

이제 이 식을 정리하자.

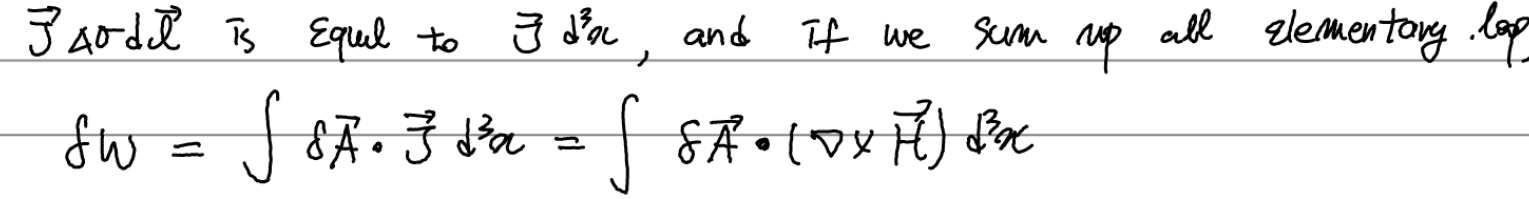
이를 다음의 vector identity를 이용하여

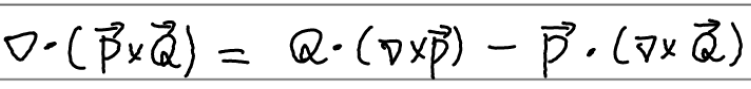
다음과 같이 정리할 수 있다.

그럼 총 W는 다음과 같다.

참고로 linear material에서 저 식이 성립하는 이유는 다음과 같다.

$$ \vec{H}\cdot\delta\vec{B}=\vec{H}\cdot\delta\mu\vec{H}=\mu \vec{H}\cdot\delta\vec{H}=\frac{1}{2}\mu(\vec{H}\cdot\delta\vec{H}+\delta\vec{H}\cdot\vec{H})$$

$$=\frac{1}{2}(\vec{H}\cdot\delta\mu\vec{H}+ \mu\vec{H}\cdot\delta\vec{H}) = \frac{1}{2}(\vec{H}\cdot\delta\vec{B}+ \vec{B}\cdot\delta\vec{H})=\frac{1}{2}\delta(\vec{H}\cdot\vec{B})$$