[잭슨 전자기학] Ch 6.1, 6.2, 6.3: 맥스웰 방정식, 게이지

( 작성일 : 2024-11-20 23:23)
Ch6 : Maxwell Equations, Macroscopic Electromagnetism, Conservation Laws

 

6.1 Maxwell's Displacement Current; Maxwell Equations

다음은 5장까지 다뤘던, 실험적으로 찾아진 공식들이다.

그러나 이들은 수학적으로 inconsistent한데, 이를 지적한것이 맥스웰이다.

이를 해결하기 위해 다음의 continuity equation에서

라는 관찰로부터,

위와 같이 displacement current를 도입하여 수정하였다. displacement current의 물리적 의미는 그리피스 참고. 학부과정에서 충분히 다루었다.

이를 통해 다음의 그 유명한 맥스웰 방정식(Maxwell's equations)이 완성되었다. 이는 이후 Herz에 의해 실험적으로 확인되었다.

이렇게 electrostatics, magnetostatics를 벗어나 확실하게 electrodynamics로 넘어왔다. 

 

실제로 맥스웰이 적은 맥스웰 방정식은 좀 더 덜 컴팩트하였다. 사원수를 이용하여 쓰였고 방정식도 20개였다. 벡터 미적분학을 이용하여 위의 4개의 방정식 꼴로 정리한 것은 헤비사이드의 작업이었다. 자세한 역사는 History of Maxwell's equations - Wikipedia를 참고.

 

6.2 Vector and Scalar Potentials

로부터, 

로부터,

로 적을 수 있다. 이를 이용하여 남은 두개의 맥스웰 방정식을 다시 쓰면 다음과 같아진다.

 

6.3 Gauge Transformations, Lorenz Gauge, Coulomb Gauge

 

임의의 스칼라함수 \(\lambda\)를 도입하여 다음과 같이 퍼텐셜을 변환해도 맥스웰 방정식은 변하지 않는다. 

즉 어떠한 \(\lambda\)를 택하더라도 물리적 실체인 장을 바꾸지 않으므로 무엇을 택하든 상관없다. 그래서 우리가 풀고 싶은 물리적 상황에 맞춰 적절한 \(\lambda\)를 택하면 문제를 쉽게 풀 수 있다. 

1. 로렌츠 게이지(Lorenz Gauge)  *Lorentz가 아님에 유의!

 

이 식 또는 이 조건을 로렌츠 게이지 조건이라고 한다. 이를 택하면 위에서 퍼텐셜을 이용해 고쳐썼던 맥스웰 방정식의 두 식을 다음과 같이 동일하고 간단한 형태(inhomogeneous wave equation 꼴)로 정리할 수 있게 된다.

 

위의 로렌츠 게이지 조건이 성립하도록 하는 스칼라함수 \( \lambda \)가 존재하는지 확인해봐야 한다. 잭슨에 나오는 간단한 유도과정을 거치면 다음을 만족하는 스칼라함수면 어떤 것이든 로렌츠 게이지 조건을 만족할 수 있음을 확인할 수 있다.

그리고 이러한 람다 하에서의 퍼텐셜들의 변환,

을 restricted gauge transformation (under Lorenz gauge condition)이라고 하며, 이를 만족하는 퍼텐셜을 로렌츠 게이지에 속한다고 한다.

이러한 로렌츠 게이지를 택하는 데에는 2가지 이유(상황)가 있다. 하나는 앞서 말했듯 맥스웰 방정식이 \(\Phi\)와 \(\vec{A}\) 둘다 동일한 구조의 inhomogeneous wave equation을 따르도록 하게 만들도록 하여 풀기 쉽게 하기 때문이고, 다른 하나는 로렌츠 게이지 조건이 좌표계에 독립적이라 특수상대론적인 고려를 하기 편하기 때문이다. 바꿔 말하면, 맥스웰 방정식이 로렌츠불변량인 space-time potential \( A^\mu = ( - \Phi /c , \vec{A} ) \) (즉, 4-vector) 에 대한 식으로 쓰이게 되기 때문이다.

 

2. 쿨롱 게이지 (Coulomb gauge) (radiation gauge, transverse gauge라고도 한다)

쿨롱 게이지 조건은 다음과 같다.

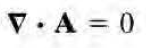
이는 위에서 계속 얘기한 두개의 맥스웰 방정식 중 첫번째 식을 다음과 같이

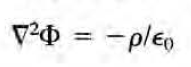
푸아송 방정식으로 만든다. 따라서 '쿨롱' 게이지라는 이름이 붙었으며, 다음의 해를 instantaneous Coulomb potential라고 부른다.

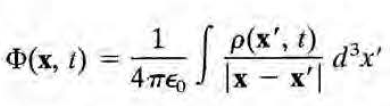
왜 'instantaneous'냐 하면 단순하게는 한 점 x에서의 시간 t에서의 퍼텐셜이 바로 그 시간 t의 모든 위치의 전하분포에 의해 결정되기 때문이고, 이것이 물리적으로 상대론을 '위반'하는 것처럼 보이기 때문에 특별히 지칭한 것이다. 물론 퍼텐셜은 물리적 실체가 아니기 때문에 상대론을 위반하는 것은 아니다. 자세한 논의는 242쪽 각주의 레퍼런스 참고.

 

두번째 맥스웰 방정식은 다음과 같이 바뀐다.

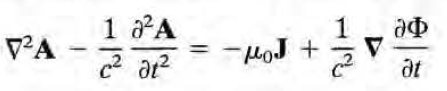
우변의 둘째항은 curl를 하면 0이 나오는데(=curlless, irrotational) 이로부터 다음의 이론을 develop한다.

우선 J를 다음의 두가지로 쪼갠다.

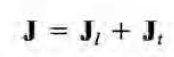
이제 이들을 다음의 두 식을 이용하여 J_l, J_t에 대한 식을 구할 수 있다고 한다.

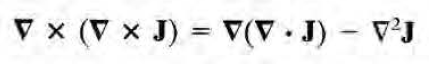
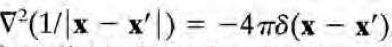
그치만 다음과 같이 E와 B의 analog로써 구할수도 있다.

이렇게 구해진 Jt, Jl은

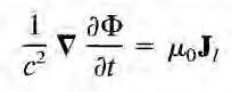
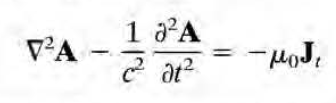
이러한 식으로 귀결된다. 따라서 벡터퍼텐셜 A는 transverse current를 source로 하는 wave로 기술되게 되며, 이것이 쿨롱 게이지를  transverse gauge라고도 부르는 이유이다.

 

쿨롱 게이지를 쓰는 상황은 source-free(rh0 =J=0)한 상황이다. 이 경우 스칼라 퍼텐셜이 0이 되고, A 또한 homogenous equation을 만족하게 된다(rho=0-> Phi=0-> J_l=0 -> J_t = J - J_l = 0). 즉 A는 plane wave로 기술된다.

이때의 전기장 및 자기장은 다음과 같이 A에만 의존하게 된다.

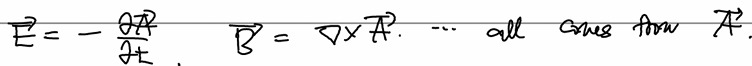
이것이 유용한 대표적인 상황은 atom-photon interaction이다. (은근슬쩍 QM으로.)

전개할 때 P dot A = A dot P이 된 부분이 있는데, 이는 쿨롱 게이지를 적용했기 때문이다.

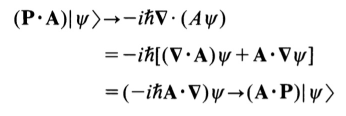
이어서, 전자기장을 다음과 같이 양자화하여 quanta로써 photon을 얻을 수 있다.

약간 대충 써져있긴 하다. 일반적으로는 벡터퍼텐셜은 모든 진동수에 대한 creation operator와 annihilation operator의 선형결합이다.  Quantization of the electromagnetic field - Wikipedia 나, 양자역학 교재에서 photon에 관한 단락을 찾아보면 조금은 보다 친절한 설명이 나온다.

따라서 이러한 연유로 쿨롱 게이지는 quantum optics(양자광학) 분야에서 자주 사용된다.