[잭슨 전자기학] Ch 5.13 : 정자기학에서의 mixed boundary problem

5.13 Effect of a Circular Hole in a Perfectly Conducting Planewith an Asymptotically Uniform Tangential Magnetic Fieldon One Side

 

정전기학에서 다뤘던 3.13절 내용( [잭슨 전자기학] Ch3 - (4/4) )의 정자기학 버전이라고 생각해도 좋다. 바꿔 말하면 정자기적 상황에서 mixed boundary problem을 풀어볼 것이다.

반지름 a의 구멍난 도체판, z>>0에 균일한 외부 자기장 H_0을 y방향으로 걸어줌.

판은 완벽한 도체: 전기전도도 \(\sigma \rightarrow \infty\), skin depth \(\delta \rightarrow \sqrt{2/\mu \omega \sigma}\) even for DC.  즉 도체 내(z=0)에는 no field

추가 가정(간단함을 위해): 판의 물질이 uniform&isotropic&linear

외부자기장으로 인해 판에 surface current가 유도되어 자기장이 생기게 될 것.

z<0 & z>0에서 전류가 없으므로, 다음과 같이 magnetic scalar potential을 적을 수 있음.

 

우변 두번째 항은 surface current로부터 만들어지는 퍼텐셜을 말함. 

계의 원통 대칭성으로부터 우변의 두번째 항을 다음과 같이 놓을 수 있음.( [잭슨 전자기학] Ch3 - (3/4) 의 (3) 참고)

asymptotic behavior는 \(y=\rho \sin{\theta}\)에 비례하게 될 것이므로, 일반식에서 m=1 항만 존재하게 되므로

lower plane(z<0)에서는 다음과 같다.

두 케이스를 합치면,

이제 경계조건을 보자.

z=0이 우리의 경계, 판이 있는 위치다. 0<=rho<a에선 판에 구멍이 뚫려있으므로 퍼텐셜이 연속적이어야 하고, rho>a에선 판이 존재하는데 이때 판에 magnetic charge가 존재한다면 퍼텐셜의 미분계수가 0이 아니겠지만 magnetic monopole은 존재하지 않으므로 0이다. \(H= -\nabla \Phi_M\)이고, \(H=B/mu\) (판의 물질을 linear로 가정했었음)임을 조합하면 수식적 유도 가능.

 

이제 식을 대입하면 다음을 얻음.

3.13절에서와의 차이점: J_1가 아니라 J_0이었고, AJ=0이고 kAJ !=0 이었다.

3.13절에서 본것과 매우 유사해보이지만 분명한 차이점이 있는 이 연립적분방정식은 다음의 알려진 해가 있다. 이 역시 3.13절에서 봤던 알려진 방정식과 해와는 다르다.

우리의 연립방정식을 위의 꼴에 끼워맞춰서 해를 구해보면 다음과 같다.

신기하게도 3.13절과 다른 방정식을 풀었는데, 초기에 외부 장을 걸어준 방향이 달라서 3.13절과 동일하게 j_1이 튀어나왔다.

 

결과에 대한 논의를 해보자. 3.13절과 동일하게 far-field는 dipole-field인데, y 방향이다. 3.13절에서는 전기장을 판에 수직인 z방향으로 걸어주었지만, 지금은 자기장을 판에 평행한 y 방향으로 걸어준 상황임을 상기. 

(그럼 왜 다른 방향으로 걸어줬느냐? 동일하게 j_1이 튀어나오게 해서 동일한 거동을 보이게 하기 위해서..)

3.13절과의 비교는 5.13절 마지막에 나와있으나 상세하진 않다. 그래도 읽어볼만하다.

 

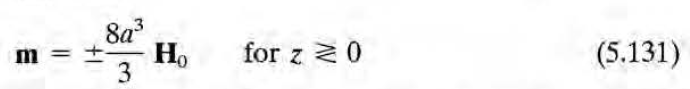
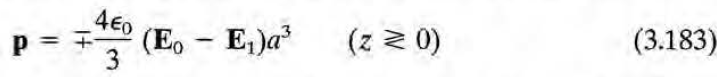
아무튼 원형 구멍을 effective magnetic dipole로 볼 수 있다(물론 far-field 기준). 

일반적인 위치에서의 자기장은 그냥 Phi_m의 그래디언트의 음수값으로부터 H를 얻고 거기에 mu0을 곱해주면 구할 수 있다. z=0일 때는 도체판 내이기에 자기장은 0이다. 특별히 z=0+ (판 바로 위)에서의 자기장은 다음과 같이 구해진다.