( 작성일 : 2024-11-29 17:27)
6.7 Poynting's Theorem and Conservation of Energy and Momentum for a System of Charged Particles and Electromagnetic Fields
전자기장 속에 전하가 존재하고, 전하가 전자기장에 의해 움직이게 될 경우 그 계의 에너지는 어떤 식으로 구해지며 어떤식으로 보존될까? 에 대한 이야기다.
우선 점전하가 속력 v로 움직이게 될 경우 다음 수식과 같이 일률은 F*v =qE*v가 될 것이다. W는 당연히 전자기장이 전하에 해준 일이 될 것이다.

즉 전자기장이 어떠한 형태로든 에너지를 가지고 있다는 얘기가 된다.
움직이는 전하는 주위의 전자기장을 변화시킬 것이고, 변화된 전자기장은 다시 전하의 움직임에 영향을 줄 것이기에 쉽지 않은 문제가 된다.
우선 다음 상황을 고려하자. 연속적인 전하 및 전류 분포를 가정하자. 부피 v 속 전하가 전자기장에 의해 받는 일의 일률은 다음과 같다.

(첫식): 점전하에선 qv였던 항이 J가 된것
다음의 두 가지 가정을 하자.
(1): linear material with negligible dispersion or losses
(2): time-varing field의 energy density 또한 \( u = (E \cdot D + B \cdot H)/2 \) 이다.
(1)에 의해 \( D=\epsilon E, H=B/\mu \) 임을 상기하여 유도하면 다음이 성립.

여기서 포인팅 벡터(Poynting vector) S를 다음과 같이 정의하고 나면 다음의 물리적 해석이 가능해진다.

u가 전자기장의 에너지였으므로 (1) du/dt는 전자기장의 에너지의 변화.
좌변은 전하가 전자기장에 의해 받는 일의 일률에 (-) 부호를 붙인 것이므로 전자기장이 전하에 의해 받는 일의 일률.
=> (2)는 부피 v의 표면을 통해 '빠져나가는' 에너지의 변화.
즉 이 식 자체가 에너지 보존법칙 그 자체이다!
양변의 적분을 벗겨 미분형으로 쓰면 다음과 같다. 각 항은 [work to fields, done by charges] or [energy of fields] per unit time per unit volume. (즉 +면 전자기장이 에너지를 얻는 것을 말하고 -면 전자기장이 에너지를 잃는 것)

기호를 바꿔 식을 다시 써보면

$$ \frac{dW_{mech}}{dt} = \frac{dE_{mech}}{dt} = \int_v \vec{J} \cdot \vec{E} d^3 x , \frac{dW_{field}}{dt} = \frac{dE_{field}}{dt} = \int_v u d^3 x $$
이 때 일의 subscript는 일을 '받는' 객체를 의미.
에너지 보존 법칙은 여기서 끝. 운동량 보존법칙을 이와 비슷한 방식으로 기술해보자.
부피 v 내 모든 입자의 운동량의 합을 \( \vec{P}_{mech} \)으로 쓰면 F= q(E+vxB)로부터 다음을 얻는다.
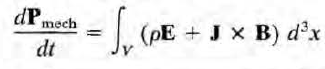
맥스웰 방정식으로 몇몇 항을 치환하면

를 얻을 수 있고, 다음과 같이 정리를 이어나가자.

(둘째 식): B의 발산은 0이기에 0을 추가한 것이므로 문제 x
이제 좌변의 둘째항과 우변의 긴 식을 정리해야할 차례다.
우선 좌변의 둘째항을, 다소 논리적 점프로 느껴질수 있지만 이를 전자기장의 운동량이라고 보자(정의하자).

그럼 위와 같이 전자기장의 운동량밀도 \( \vec{g} \) 또한 정의할 수 있다.
이제 우변을 정리하자.
깔끔하게 정리하고 나서 해도 되지만, 어차피 결론은 동일하니까.. 다음과 같이 electromagnetic tensor, 더 잘 알려진 이름으로는 맥스웰 변형 텐서(Maxwell stress tensor)를 정의하자.

이 텐서가 우변과 어떻게 관련되는지는 다음을 보자.
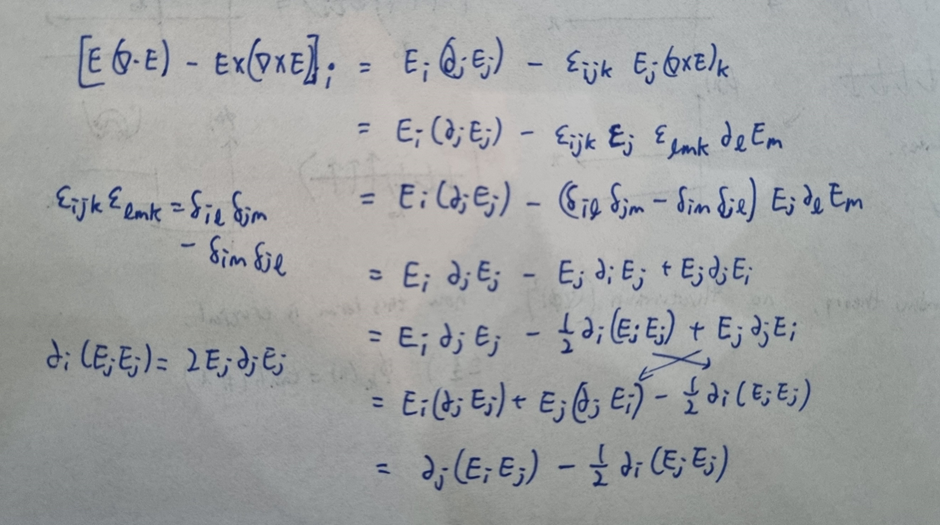

자기장의 경우는 계수만 다를뿐 동일한 식의 구조를 가지고 있으니 생략.
따라서 우리의 첫식은 다음과 같이 정리된다.
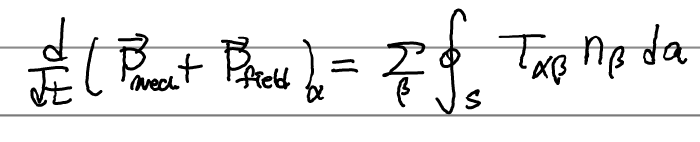
\(n_\beta \)는 표면의 법선벡터로, 발산정리를 적용한 것이다.
이 식을 다른 꼴로 쓰자면 다음과 같이도 쓸 수 있다. (왜 굳이 없던 마이너스 부호를 만들어 꺼냈느냐- continuity eqn 꼴을 만든것)

T 위의 양방향 화살표는 텐서임을 나타내는 표기이다. (그러나 텐서의 rank를 표현할 수 없기에 자주 사용되지는 않는다)
그리고 운동량의 시간미분이 힘이라는 것을 생각하면, 이는 곧 뉴턴의 제2법칙이기도 하다!

이런 이야기도 할 수 있긴 하나 크게 중요하진 않다. 전하가 없어 mechanical한 힘이 가해질 수 없는 상황에 대한 이야기.
continuity equation, 연속 방정식과의 관계도 꼭 언급해야할 주제. 그치만 기억해야할건 운동량 출입 시 부호 딱 한가지.
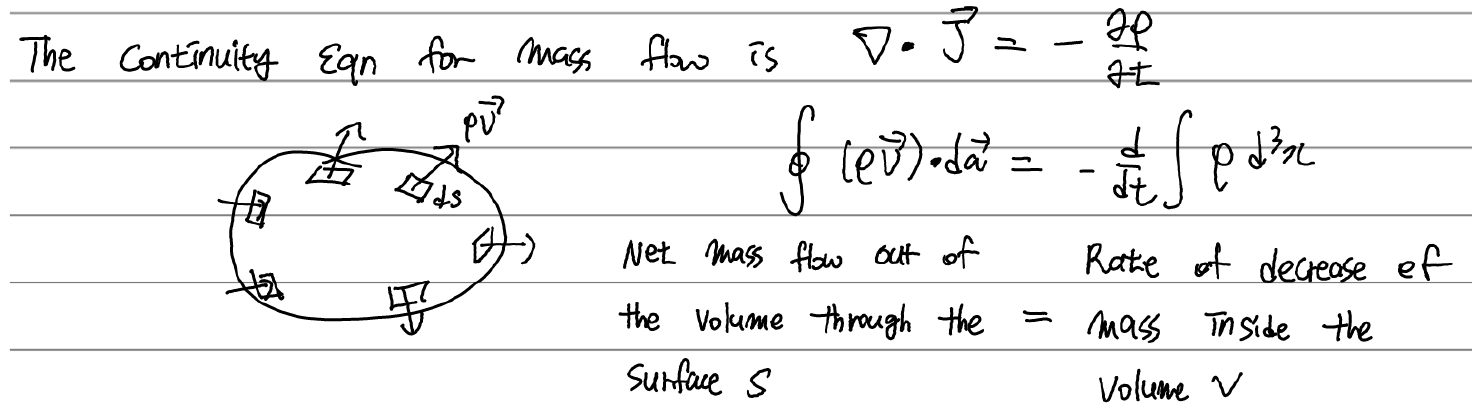
이를 상기해서, 다음과 같이 T dot da 의 부호가 양수면 계 내로 운동량이 들어오는 것임을 알 수 있다.

다음으로는 전자기장이 가하는 힘에 대한 이야기다. 앞서 언급했듯, 운동량 보존법칙을 시간미분하면 뉴턴의 제2법칙이 나온다.
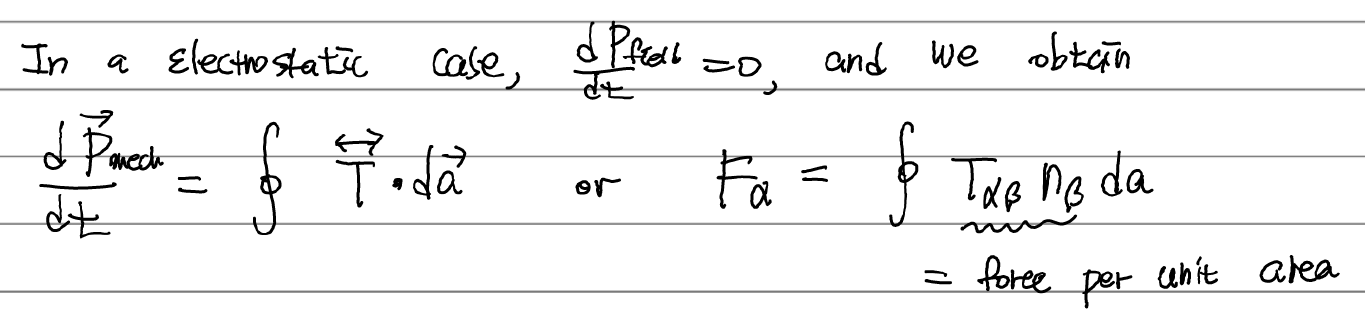
따라서 맥스웰 변형텐서 T를 이용해 force를 구할 수 있다. electrostatic한 경우 전하가 받는 힘이 직접적으로 계산되고, dynamic한 경우 좌변에 전자기장이 받는 힘 또한 포함되기 때문에 실제 물질이 받는 힘을 바로 구할 수는 없고, field에 의한 힘까지 고려해야 하며 다음과 같이(per unit area) 구해진다.
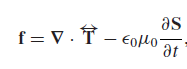
예시:

그리피스 8장에 나오는 예시다. 마지막에 텐서를 구하는 부분이 너무 생략되어 있으니 대충 볼것
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 7.1~7.4: 전자기파의 도입 (0) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.6 : 미시적 관점으로부터 맥스웰 방정식 유도 (0) | 2024.12.06 |
| [잭슨 전자기학] ch 6.5: 움직이는 점전하가 만드는 전기장과 자기장 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.4 : 로렌츠 게이지 하의 맥스웰 방정식을 풀기 위한 시간 의존적 그린 함수 (0) | 2024.12.06 |