[잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화

6.11 On the Question of Magnetic Monopoles

2024년 기준으로 magnetic monopole(자기홀극)의 존재는 실험적으로 검증되지 않았다. 그러나 이론적으로 존재할 것이라는 심증이 몇가지 존재한다. 바꿔 말하면, 이론적으로 자기홀극이 존재하지 않을 이유가 없다.

 

1) 맥스웰 방정식의 비대칭성의 해결

magnetic 'charge'가 존재한다면 다음과 같이 대칭적인 구조를 갖게 될 수 있다.

2) 맥스웰 방정식의 ambiguity로 인한 가능성

다음과 같은 field의 transformation과 source의 transformation을 고려하자.

transformation의 구체적인 결과는 다음과 같다.

따라서 우리가 어떤 입자의 거동만을 보고서는 이것이 electric charge인지 magnetic charge인지 판단할 수 없다. 즉 ${\rho }_m=J_m=0$이 되도록 하는 $\xi$를 항상 찾을 수 있다. 이것이 우리가 지금까지 magnetic charge를 발견하지 못한 원인일 수 있다.

다만 이 논의의 문제는 자하와 전하 값의 비율이 고정되어 있을 거라는(그리고 그 값이 매우 0에 가까울 것이라는) 우리의 경험적 추측과는 달리 $\xi$의 값에 따라 임의의 값을 가질 수 있다는 것이다. 그래서 일반적인 물질들은 electric charge만 지니는 것일 수 있다. 그럼에도 불구하고 unstable한 입자들은 magnetic charge를 가질 가능성이 열려있고, most unified theory of the fundamental forces는 자하의 존재를 예측한다.

 

3) 전자의 양자화 설명 가능

다음절에서.

 

잭슨은 마지막으로 다음과 같은 논의를 한다. g는 자기홀극의 magnetic charge를 말한다.

(오타가 있다. $\alpha n^2/4$가 아니라 $n^2/4\alpha$이다.)

5000이란 값은 34*1^2/(1/137)=4658~5000으로부터 계산된 값. 중간에 쓰인 Dirac's quantization condition은 바로 다음절, 아래에서 논의한다.

 

잭슨엔 좀 더 디테일한 논의들이 있으나 적당히 요약하여 가져왔다. 사실 반쯤 재미로 보는 파트고 크게 중요한 부분은 아니니까.

 

6.12 Discussion of the Dirac Quantization Condition

 

왼쪽 그림과 같이 매우 긴 솔레노이드를 생각하자. 솔레노이드의 far-field는 magnetic dipole field이기 때문에  솔레노이드의 양 끝이 매우 멀리 있으면 각 끝을 magnetic monopole로 생각할 수 있다. 

그래서 아래와 같이 continuous dipole string(string theory의 string 아님..)을 고려하여 벡터퍼텐셜을 계산하면 다음과 같다.

 

delta(y)는 string임을 의미.

 

만약 자기홀극이 이런 식으로 존재한다면, 두개의 자기홀극을 잇는 continuous magnetic string이 존재할텐데, 이 string은 우주 속에서 어떤 식으로 존재할 수 있을까? 또, 전자가 이 string과 만나면 어떤 일이 벌어질까? 처음에 디랙은 전자의 파동함수의 값이 string과 만나는 곳에선 0이 되어 전자가 string과 상호작용하지 않을 수 있을 것이라 생각했지만 이는 곧 반박당했으며, 디랙은 곧 다음의 이론을 생각했다.

다음의 게이지 변환과 엮어 생각하면 guage function과 \(\Omega)의 관계식을 얻을 수 있다.

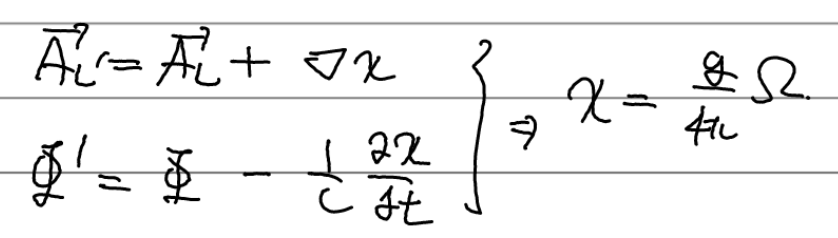
게이지 변환 후 전자기적 퍼텐셜이 변하더라도 장은 변하지 않고 따라서 전자의 파동함수도 변하지 않아야 하므로 

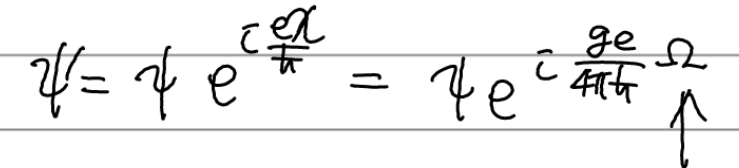
위의 지수가 2pin이어야 한다.

전자가 위의 L과 L' 이 만드는 면의 바로 앞에서 바로 뒤로 이동하게 되면 solid angle $\mathrm{\Omega }$는 2pi에서 -2pi로 바뀌게 되는데, 이는 다음의 결과가 성립해야함을 의미한다. (그러지 않으면 전자의 파동함수가 multi-valued가 되어 비물리적이게 된다)

$$\frac{ge}{4\pi \hslash }4\pi =2\pi n\to \frac{ge}{\hslash }=2\pi n\text{(n is integer)}$$

 

이상의 논의는 David Tong의 quantum hall effect에 관한 강의노트에도 실려있다. David Tong: The Quantum Hall Effect