( 작성일 : 2024-11-28 15:21)
6.5 Retarded Solutions for the Fields
이제 실제 물리적 상황을 하나 풀어보자. 일정한 속도로 움직이는 점전하가 만드는 전기장과 자기장을 구해보자.
로렌츠 게이지 하에서 맥스웰 방정식은

앞선 6.4절에서 구한 retarded solution를 적용하면 퍼텐셜은 다음과 같이 구해진다.

(A는 벡터라지만 component별로 따지면 Phi에서와 동일하고, 각 component별로 구한 뒤 다시 벡터 꼴로 합쳐 쓴거라고 보면 된다.)
이로부터 바로 E와 B를 구할 수 있다. 그러나 이번 절에서는 조금 다르게, 보다 직접적으로 구해볼 것이다.
우선 다음과 같이 정리해보자.

그럼 E와 B가 마치 바로 전에 봤던, Phi와 A가 만족하던 inhomogeneous wave eqn과 같은 꼴이 된 것을 볼 수 있다.
따라서 바로

와 같이 해를 적을 수 있다.
여기서 유의할 점은

라는 점이다. 길게 설명할 필요 없이, 다음을 보면 된다.

둘째 줄의 첫 항은 \( \partial / \partial x' \)이 \( \rho(x', t') \)의 x'에 적용되었을 때 나오고, 둘째 항은 \( \rho(x', t') \)의 t'에 적용되었을 때 나온다. 그래서 둘째 항이 저렇게 두 항의 곱으로 나온 것이다. 다음처럼 보는게 보다 이해가 빠를 것이다.

왜 \( \nabla [ \rho ]_{ret} \) 는 전미분 d/dx에 해당되고, \( [ \nabla \rho ]_{ret} \) 은 편미분 \( \partial / \partial x \)에 해당되는지 의아할 수 있는데, retarded time을 집어넣는 타이밍이 언제인지 곰곰히 생각해보면 쉽게 이해할 수 있다. ret를 먼저 취하고 미분(del)한다는 것은 rho의 시간 항에 x 의존성을 넣은 뒤 미분한다는 것이므로 전미분이 되고, 미분을 먼저하고 ret를 취하는 것은 시간 항에 x 의존성이 없는 상태로 미분한 후 시간 항에 원래 넣어야할 시간(retarded time, t-R/c)을 넣어주는 것이므로 편미분이 되는 것이다.
유사한 방식으로 J의 curl에 대해서도 다음과 같이 계산 가능하다. (좌변의 세로바는 오타이므로 무시)

이제 거의 끝났다. 위에 구해놨던 field의 retarded solution에 대입하기만 하면 된다.

우선 전기장부터 하면,

(두번째 식은 평범한 부분적분. 다만 우변의 첫 항을 계산할 때 다음의 살짝 낯선 공식을 써야한다.)

다음으로 자기장은,
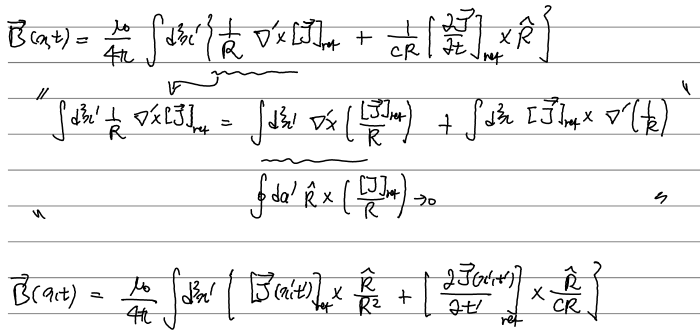
(두번째 식은 약간 낯선 형태의 부분적분. 우변의 첫항을 계산할 때도 다음의 살짝 낯선 공식을 써야한다.)
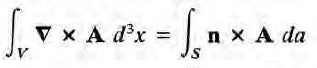
이렇게 구한 E와 B 두 식을 두고 Jefimenko's generalization of the Coulomb and Biot-Savart law라고 부른다. ( 예피멘코 방정식 - 위키백과, 우리 모두의 백과사전) 유도할 때 그린함수를 쓰지 않았을 뿐, 학부 교재인 그리피스에서도 나오는 식이다.
이제 처음에 언급했던, 일정한 속도로 움직이는 점전하가 만드는 전기장과 자기장을 구해보면 다음과 같다.
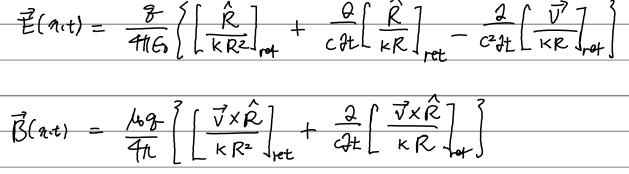

유도 과정을 쓰기에 앞서, 물리적 상황을 잠시 생각해보자. (x,t)의 장에 영향을 미치는 소스(점전하)는 그로부터 거리는 R만큼, 시간은 R/c만큼 떨어져 있다. 그러나 주어진 상황에서 점전하는 계속 움직이고 있기에 시간 t-R/c에서의 전하의 위치와 t에서의 위치는 다르다. 상황을 그려보면,
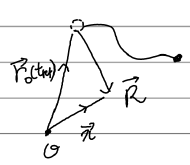
원점 O, 위치 \( \vec{R} \) : 우리가 장을 구할 위치, 위치 \( \vec{r_o} ( t_{ret} ) \): 위치 R의 장에 영향을 끼치는 과거의 점전하의 위치이다. 이 점으로부터 곡선으로 이어진 검은 점은 현재의 점전하를 말하는 것으로 이미 그 위치에서 벗어낫음을 의미.
이제 유도를 시작하자.
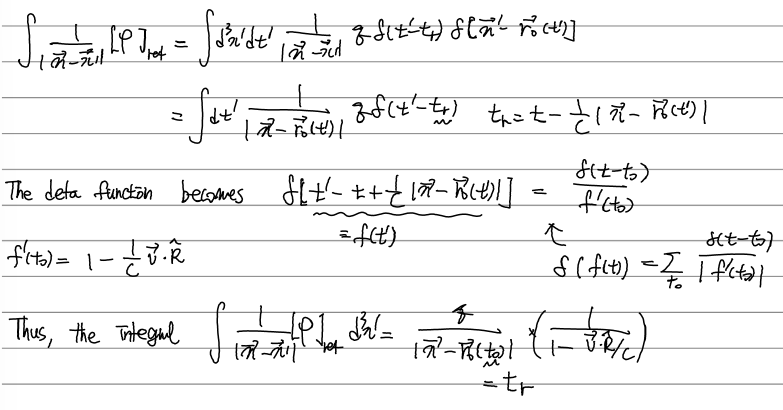
첫 줄에서는 \([\rho]_{ret}\)이 다음과 같음을 이용한 것이다. ret를 평가하는 것을 시간에 대한 델타함수로 표현한 것.
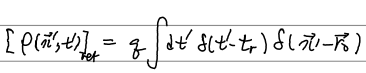
딱 하나 사소한 오류가 있는데 맨 마지막 식에서 t_0=t_r이라 써놨는데, t_r 정의에 t'이 들어있어서 이렇게 쓰면 안된다. 그냥 f(t')=0의 해로서 정의되는 t_0에서 마무리 짓는게 수학적으로 깔끔하다. 다만 아래 사진에 그려놓은 것처럼 t_0는 위치 x에 영향을 주는 소스의 시간이라는 물리적 의미가 있다. 그런 의미에서 retarded를 의미하는 index을 붙여줄 수는 있다.
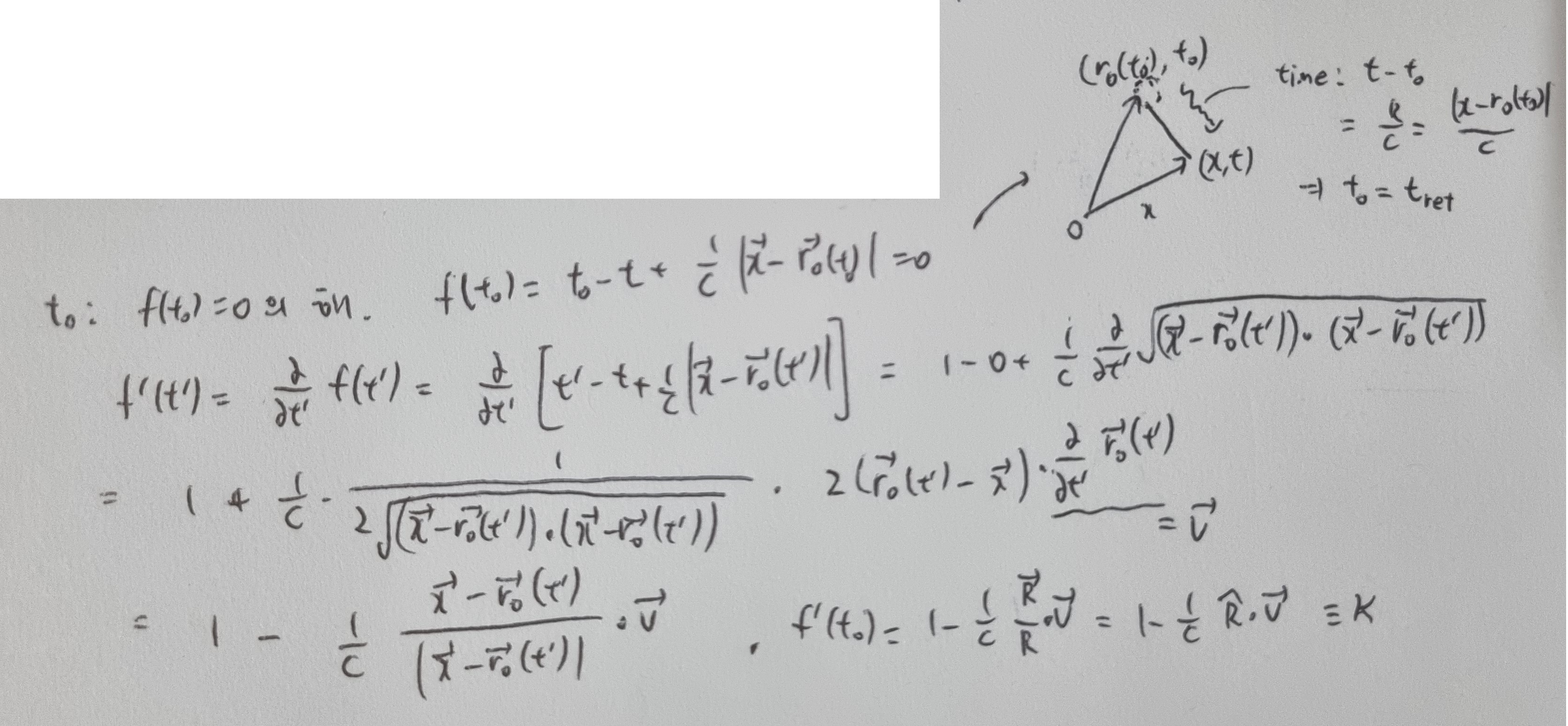
위 사진은 델타함수 관련 계산을 보충하는 수식.
말하지 않았지만 지금까지 구한 것은 일정한 속도로 움직이는 점전하에 대한 것보다 살짝 더 일반화된 식이다. 사실은, 움직이는 점전하에 대한 일반적인 식이다! 가속해도 되고, 직선운동하지 않아도 된다. 그러나 그럼 살짝 불안해지는데, 점전하의 가속이 허용되는 순간 특수상대론을 벗어나는 것 아닐까 싶기 때문이다. 이 불안감은 절반만 사실로 드러난다. 고등학교에서도 배우다시피, 전하가 가속하면 전자기파를 주위에 방출하며 에너지를 잃는다. 이를 radiation이라고 하며, 학부 전자기에서도 배운다. 여기서 구한 전자기장을 이용하여 가속하는 점전하의 radiation을 계산해보면, 점전하가 스스로에게 힘을 가해 가속시킨다는 괴랄한 결론을 얻게 된다. 고전 전자기학이 점전하를 잘 설명하지 못하는 부분. Abraham–Lorentz force - Wikipedia (추후 보충)
kappa에 대한 물리적 해석과, 일정한 속도로 움직이는 경우에 대한 계산과, 그에 관한 특수상대론적 논의는 그리피스 10.3절 참고.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 6.7 포인팅 정리: 전자기장과 전하 계의 에너지 보존정리 (0) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 6.6 : 미시적 관점으로부터 맥스웰 방정식 유도 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.4 : 로렌츠 게이지 하의 맥스웰 방정식을 풀기 위한 시간 의존적 그린 함수 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.1, 6.2, 6.3: 맥스웰 방정식, 게이지 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 5.15, 5.16 : 패러데이의 법칙, 자기장의 에너지 (0) | 2024.12.06 |