수식이 많아진다....
3.1 Laplace Equation in Spherical Coordinates

구면좌표계에서 변수분리는 다음과 같이 한다.

대입 후 정리;

변수가 분리되어 뒷항은 상수여야만 하고, 그 상수를 다음과 같이 정의


관심 영역이 전체 phi를 포함할 경우 ("full azimuthal range is allowed") Q(phi) = Q(phi+2pi) 구속조건이 생기고(한점에서의 퍼텐셜의 유일하게 결정되어야 하기에), 이 구속조건 하에서 m은 정수여야 한다.
이제 U랑 P도 변수분리하자. 상수 l을 도입해 다음과 같이 분리할수 있다. (왜 하필 l(l+1)로 썼는지는 다들 알것)

두번째 미분방정식을 풀면 다음과 같다.

3.2 르장드르 다항식
전자기학, 양자역학, 수리물리 때 다루는 아주 낯익은 특수함수. 잭슨 책은 물론이고 수리물리 교재를 펴도 나온다.
다음의 링크를 참고해도 좋다. 조금은 느리게 살자: 르장드르의 미분 방정식(Legendre's Differential Equation) (ghebook.blogspot.com)
(1)

이 방정식 이름은 generalized Legendre equation이고, 해는 associated Legendre polynomial이다. m이 정수임은 언급했었고, l은 0 이상의 정수이다. (사실 l이 정수가 아녀도 된다. 다만 이 경우 해가 polynomial이 아닌 무한급수로 나오게 되고, 이 경우의 해는 (associated) Legendre function이라고 부르게 된다. 더 자세히는 무한급수를 가정하여 풀어나오는 해를 제 1종(first kind), 이 해와 선형독립인 두번째 해(2계 미분방정식임을 상기할것)를 제 2종(second kind)이라고 부르게 된다.)
(2)

위 방정식에서 m=0인 케이스. 방정식의 이름은 Legendre equation이고, 해는 Legendre polynomial이다. l은 0 이상의 정수.

(associated) 르장드르 다항식의 정의역은 -1<= x <=1이다.
잭슨에서는 수리물리책마냥 해를 어떻게 구하는지 일일히 설명하는데, 다 아는 내용이니 생략.
그래도 성질이나 공식 몇가지만 복붙하면 다음과 같다.
(1) 로드리게스 공식

(2) 직교성

이로부터 -1<=x<=1 사이의 임의의 함수를 르장드르 다항식의 선형결합으로 나타낼 수 있다.

(2-1) step function의 Legendre series expansion
소개 안해도 되는 예시이긴 한데, 문제 풀이 중에 이 결과가 한번 쓰이는 경우가 있어서 괜히 한번 소개한다.


(3)
P_l (1) = 1 for all l (사실 이건 성질이 아니라 정의다. 일종의 규격화 조건.)
P_l (-1) = (-1)^l
P_l(x) = (-1)^l * P_l(-x)
P_l(0) = 0 for even l
P_l(0) for odd l : Legendre polynomial with argument zero $P_n ( 0 )$ - Mathematics Stack Exchange
(4) 잡다한 점화식
여기 쓰진 않겠지만 문제 풀이에 있어 중요하게 쓰인다. 가령 르장드르 다항식을 미분한 식을 정리해야할 때가 있는데, 이 때 점화식을 이용하여 두 르장드르 다항식의 차 형태로 간단하게 정리할 수 있다. 문제 3.2 참고.
(5) 위의 점화식으로부터 얻어지는 자잘한 공식. 가~끔 써야할 때가 있다. (쓸일이 없길 바란다)


(뒤의 조건을 만족하지 않는 l, l'에 대해서는 식의 값은 0이 된다)
(왼쪽 식은 두 경우가 사실 같은 식인데 왜 저렇게 따로 케이스를 나눈건지 잭슨의 의도를 모르겠다)
르장드르 방정식을 소개하는 이유는 위의 P(theta)에 관한 미분방정식이 다음의 치환을 통해 르장드르 방정식으로 환원될 수 있기 때문이다.
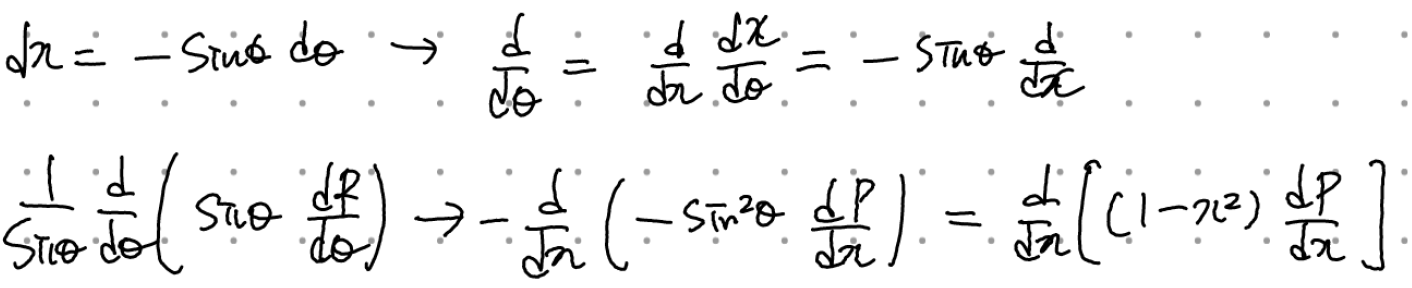
이로부터 위의 P(theta)는 (m=0일 때) P_l(cos theta)가 됨을 알 수 있다.
(6) 참고할만한 자료
-아프켄 등 수리물리
-잭슨
- Chapter 3: Legendre Polynomials | Physics (uoguelph.ca)
3.3 Boundary-Value Problems with Azimuthal Symmetry(원통대칭)
원통 대칭성(=방위각 대칭성)에 대한 친절한 설명: 편미분방정식에 변수분리법을 쓸 때 방위각 주기성, 방위각 대칭성의 뜻(What does azimuthal periodic, and azimuthal symmetric stand for?) (tistory.com)
이제부터 본격적으로 숨이 막혀온다. 그래도 가끔 흥미로운 결과들이 등장하니 참아보자. (독자에게 하는 말이 아니라 본인에게 하는말.. 자기세뇌를 하고있다)
z축 원통대칭성이 있는 경우, phi 값이 달라져도 퍼텐셜의 값이 바뀌지 않으므로 위에서 구한 일반적인 식을 이용하여 퍼텐셜을 다음과 같이 쓸수 있다. 이때 원통대칭성을 다루고 있음에도 식의 변수들이 원통좌표계가 아닌 구면좌표계의 변수임에 유의하라.
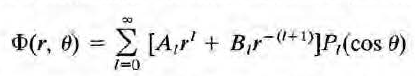
Q(phi)가 상수이기 위해선 m=0이어야만 한다. 이로 인해 P(theta) 파트도 associated 르장드르 다항식에서 르장드르 다항식으로 바뀐걸 볼 수 있다.
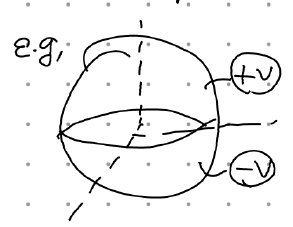
전에 다뤘던 상황을 다시 가져왔다. 얘는 z축 (원통)대칭성이 존재한다. 원점에 전하가 없을 경우 퍼텐셜이 finite한 값을 가져야하고, r=0에서 발산하는 항이 사라져야하기 때문에 B_l =0 (for all l)이 되어야 한다.
이를 대입하면
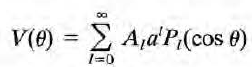
계수 A_l을 결정하기 위해 양변에 르장드르 다항식 곱하고 적분, 직교성 이용해 A_l을 쓰면
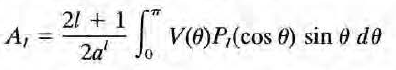
이제 경계조건
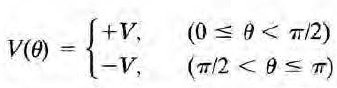
을 대입하면 다음의 퍼텐셜을 얻을수 있다. 와~
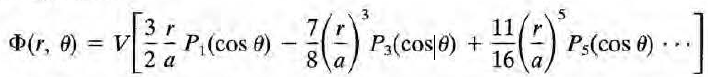
그리고 이 식은 (2.27)의 interior 버전이다. (관심 영역이 구 밖일 때의 퍼텐셜 식이 2.27, 구 안일 때 식이 지금 구한 식이라는 이야기. 이 둘 간의 conversion 방법이 잭슨 본문에 간단히 나와있으며, 이는 문제 2.22번에서도 볼 수 있다)
그리고 직관적으로 보이는 한가지 꼼수가 정당화될 수 있다는 매우 신기한 이야기가 나온다. 바로 대칭축에서의 퍼텐셜만 알아도 관심 영역 전체의 퍼텐셜을 구할 수 있다는 이야기다. 딱 P_l(cos theta)만 곱해주기만 하면 된다. (이 때 축에서의 퍼텐셜은 값이 아니라 식을 알아야 한다. 각 l마다 항을 집어넣어줄 것이기 때문)
이게 가능한 이유는 다음과 같다. z축에서의 퍼텐셜은 다음과 같다. (P_l(1) =1 for all l 이므로)

(z가 음수일 때는 (-1)^l 이 곱해져야 한다. P_l(cos pi) = P_l(-1) = (-1)^l이므로)
여기에 P_l(cos theta)를 곱하면 바로 원통대칭성이 있을 때의 퍼텐셜의 일반식이 나온다.
실제 적용 예시를 보자.
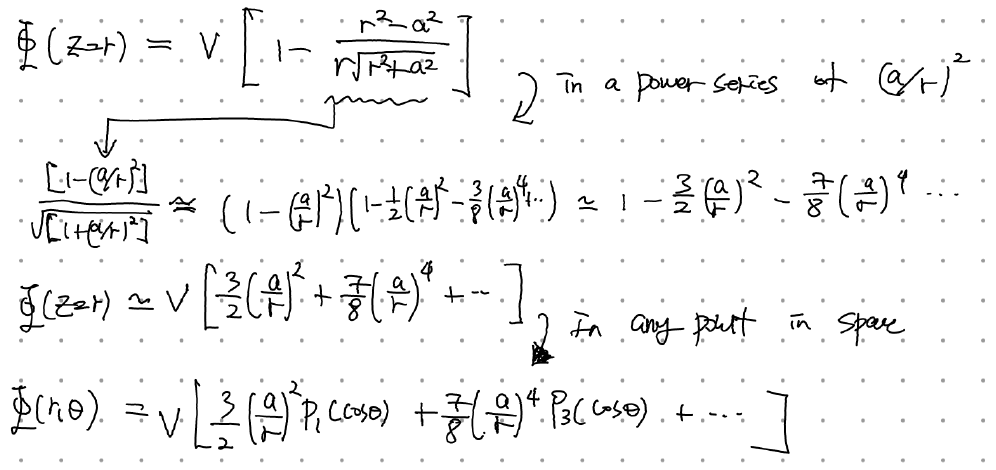
축에서의 퍼텐셜을 r의 거듭제곱으로 전개하여 l 별로 분리해내는게 포인트. 교재에서는 아예 일반식을 가지고 놀아서 한눈에 안들어온다.
이제 또 하나의 신기한 공식을 볼 차례다.
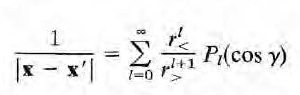
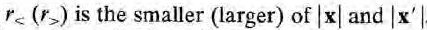
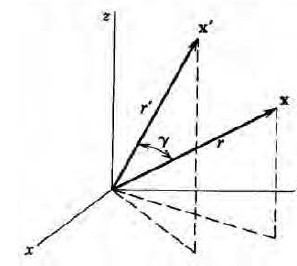
우선 x'의 방향을 새로운 z축으로 잡는다. 그러면 1/|x-x'|은 z축 원통 대칭성을 갖게 되고, 위에서 구한 일반식을 쓸수 있다. ( 1/|x-x'|을 위치 x의 퍼텐셜로 바라보는 것이다)
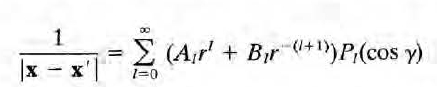
이제 x가 z축 위에 있다(x'과 같은 방향으로 놓여있다)고 가정하자. (혹은 z축 위의 한 점을 골라다 x로 삼자) 그럼 gamma = 0이 되므로 우변은
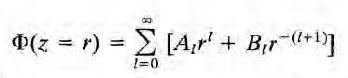
이 되고, 좌변은
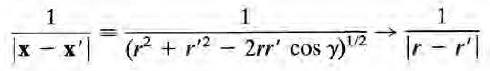
이 된다. 직관적으로도 당연한 결과. 합쳐서 써보면 다음과 같다.
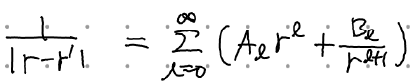
아래의 과정을 거치면,
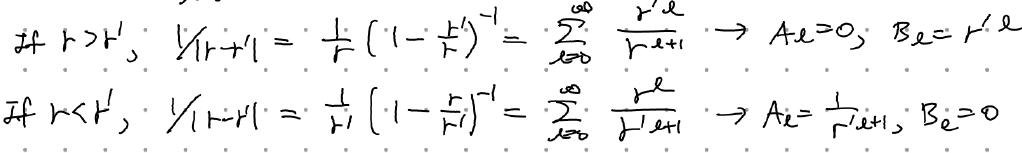
다음과 같이 정리할 수 있다.
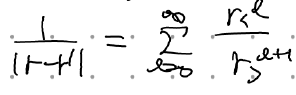
지금 이 식은 x가 z축 위에 있을 때의 것으로, 대칭축에서의 퍼텐셜 식을 구한 것과 다름없다. 따라서 르장드르 다항식을 곱하면 전체 공간에서의 퍼텐셜을 구할 수 있게 된다. 즉,

이 성립한다. ( 더 이상 x는 z축 위에 있을 필요없이, 임의의 위치로 일반화되었다.)
바로 이어서 이를 적용하는 예시가 나온다.
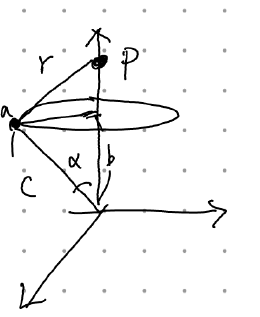
위와 같이 생긴 대전된 ring이 만드는 퍼텐셜을 구하는 문제이다. 복잡한 적분을 할 필요없이 순식간에 구할 수 있다.
z축 대칭이네 -> 생긴거 보니 z축에서의 퍼텐셜은 구하기 쉽겠네 -> 어라 대칭축에서의 퍼텐셜을 알게 됐으니 전체 공간의 퍼텐셜은 르장드르 다항식만 곱해주면 바로 나오네 의 과정을 거치면 된다.
z축에서의 퍼텐셜은
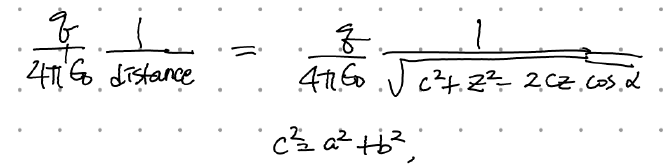
으로 쉽게 구해지는데, 저 1/distance라는 녀석을 우린 이미 바로 위에서 구했다.
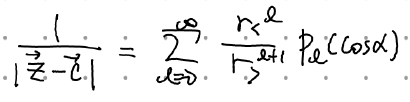
(이때 r_> = max(z,c), r_<= min(z,c) 이고, alpha는 고정된 상수)
따라서 전체 영역의 퍼텐셜은 다음과 같다.

3.4 Behavior of Fields in a Conical Hole or Near a Sharp Point
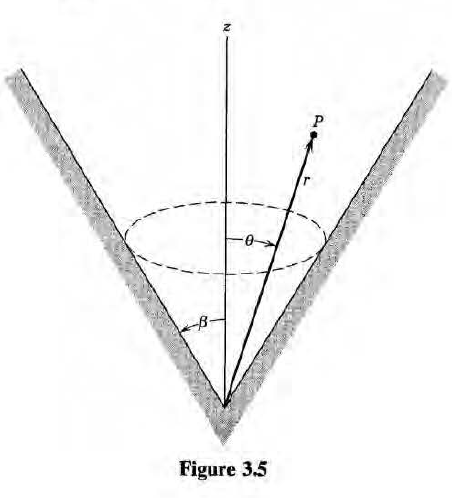
원통대칭성이 있으나 모든 theta가 cover되지 않는 상황이다. 이 경우 P_l(cos theta) (l은 정수)는 힘을 잃게 된다. 왜냐.. 가 좀 까다로운데, 우리가 르장드르 다항식을 구할 때는 일반적인 무한급수(series of x^n)를 가정하고 이를 미분방정식에 대입해 각 order마다의 계수가 이루는 점화식을 구하고, 적절한 값을 넣어 계수를 구했었다(프로베니우스 방법). 그러나 지금의 상황 같은 경우, x=0이 관심 영역 내에 포함되지 않는다. 따라서 처음에 가정한 무한급수의 꼴을 바꿔야만 한다. x^n 들의 합으로 뒀다는 것 자체가 x=0에서의 regularity를 가정한 것이기 때문. 그래서 우리는 x=1에서의 regularity를 가정하고 (즉 적어도 theta=0은 관심 영역 내에 있는 상황을 가정하고), 보기 편한 변수를 새로 설정하여 거기서 다시 무한급수를 가정하여 미분방정식을 풀 것이다. 그러면 동일한 미분방정식을 풀지만 l이 정수가 아닌 수가 될 수 있게 된다. 그리고 이 때의 해를 르장드르 함수라고 한다. (르장드르 다항식에서 르장드르 함수로 바뀜)
정리하면,
l이 0 이상의 정수 => 계수간 점화식이 어느 순간에서 끝남 => 해가 무한급수가 아닌 다항식이 됨 = 르장드르 다항식. 이 경우 -1, 0, 1을 포함한 모든 실수에서 regular. 바꿔말하면 1에서도 -1에서도 regular하기 위해선 l이 0 이상의 정수여야만.
l이 정수가 아님 => 계수간 점화식이 안 끝남 => 해가 무한급수가 됨 = 르장드르 함수. 이 경우 1에서는 regular 하지만 -1에서는 (항상) singular. 그래서 -1이 제외되는 상황(theta=pi가 관심영역 밖)이면 l이 정수가 아니어도 됨.
위에 써논 내용 중에 틀린 부분이 있을 수 있으니 궁금한 사람은 고오급 수리물리책을 뒤져보거나 다음의 링크를 참고할것. Legendre function - Wikipedia 잭슨도 완벽하게 regularity에 대한 논의를 서술해놓지는 않았다.
여튼 이런 경우 퍼텐셜의 일반해는 이런식으로 쓰일 수 있다고 한다. v_k가 뭔지는 잭슨 본문 참고.
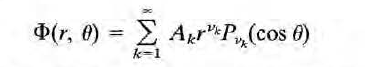
본문에서 경계조건 적용해서 직접 풀고 뭐 어디 근처에서 르장드르 함수를 베셀함수로 근사해서 전기장 구하고 이러는데 정독은 안했다. 중요하지 않으니 넘어갈 예정. (이런 건 공부를 하든 연구를 하든 하다 중요해지게 되면 그때 가서 공부해도 된다.)
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch3 - (3/4) (0) | 2024.10.02 |
|---|---|
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch2 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (2/2): 푸아송 방정식, 라플라스 방정식, 그린함수, 경계조건 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (1/2): 전기장, 전위, 가우스법칙, 쌍극자층 (0) | 2024.09.29 |