원통좌표계를 다루는 3.7, 8, 11절을 묶어서 다뤄보겠다.
논리 흐름은 구면좌표계에서와 다를게 없다. 단지 쓰이는 특수함수가 르장드르에서 베셀함수로 바뀔 뿐이다.
수리물리 시간에 보통 스킵하는 함수인 한켈 함수 같은 것도 보게 된다.
<등장하는 특수함수 정리>
1) 베셀 방정식 Bessel equation
$$ \frac{d^2 R}{dx^2} + \frac{1}{x} \frac{dR}{dx} + (1- \frac{\nu^2}{x^2}) R = 0 $$
이 방정식의 해가 Bessel function이 된다.
2) (제 1종) 베셀 함수 Bessel function (of the first kind of order ±v)

v가 정수가 아닐 때 이 둘은 선형독립이다. (즉 미방 풀이 끝, 해를 더 찾을 필요 없다 - 베셀 방정식이 2계 미분방정식임을 유의)
그러나 v가 정수면 다음의 관계
$$ J_{-m} (x) = (-1)^m J_m (x) $$
를 만족하게 되고, 선형독립이 아니게 된다. 즉 해를 더 찾아야 한다.
3) 노이만 함수 Neumann function (=제 2종 베셀함수 Bessel function of the second kind)

그 해가 바로 이것. 그래서 베셀 방정식의 일반해는 J_v(x)와 N_v(x)의 선형결합으로 쓸 수 있다(심지어 v가 정수일지라도. 확인해보면 알겠지만 v->integer의 경우일지라도 N_v(x)는 J_v(x)와 선형독립이기 때문이다)
4) 한켈 함수 Hankel function (= 제 3종 베셀함수 The Bessel functions of the third kind, 자주 쓰이는 표현은 아님)

단순히 선형결합일 뿐이기에 수학적으로는 그리 큰 의미는 없다.
5) 점화식

Omega_v(x) 자리에
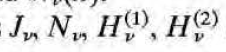
중 뭐가 들어가도 성립한다.
6) 극한에서 함수의 거동
leading term만 적었다.

이때 0.5772..는 오일러-마스케로니 상수.

이 두 거동의 경계는 x~v에서 나타남.
7) 베셀 함수의 근(root)
무한히 많다. 게다가 무리수. 그래서 다음과 같이 기호로 나타낸다.

x_vn이란 order v의 베셀함수의 n번째 근이라는 뜻.
다음은 몇가지 예시.

n이 클 경우 다음과 같은 근사식이 있다.

8) 직교성
뒤에서 설명하겠지만 베셀함수를 통해 원통좌표계에서의 라플라스 방정식의 해의 radial part를 설명할 것이다. 그래서 베셀함수의 직교성이 중요하다. 여기서 우리는 제 1종 베셀함수만을 다룰 것.
다음의 함수가 0<= rho <= a에서 orthogonal set을 이룬다. (v>=0이라고 써있지만, 실제로는 v>=-1에서도 성립)

다음과 같은 orthogonality condition이 성립하기 때문. (유도과정은 잭슨에. 아프켄에서도 안보였던걸..)

따라서 0<=rho<=a에서의 임의의 함수를 다음과 같이 표현 가능(conventional Fourier-Bessel series - 푸리에 급수에서 basis로 cos sin을 썼듯 basis를 베셀로 해서 함수를 급수형태로 표현하겠다 해서 푸리에-베셀 급수).

9) 위의 f(rho)는 rho=a에서 0이 된다. 이는 디리클레 조건과 잘 맞음. 그러나 다른 방식의 전개도 가능하다.

를 이용하여 전개하는 것. 이게 가능한 이유는 위의 orthogonality condition을 유도할때

의 값이 end point rho=0과 rho=a에서 0어야 한다는 조건을 썼기 때문이다. 따라서 x_vn이 아닌 y_vn 버전의 식을 사용해도 orthogonality condition이 만족되고, basis로 쓸 수 있다.
이 함수의 set을 basis로 하여 전개할 경우, rho=a에서 f(rho)의 미분값이 0이 된다. 이거에 걸맞는 경계조건이 주어지는 상황이면 이 전개를 택하면 될 것. 즉 노이만 조건이고 표면에 수직한 전기장이 항상 0일 경우 이를 쓰면 될 것이다.
10) modified Bessel functions
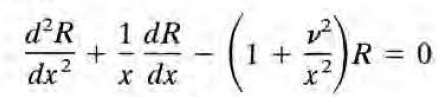
이 방정식의 선형독립인 해로 보통 다음을 택한다. 이러면 두 함수가 (실수 v에 대해) 실함수가 된다.
$$ I_{\nu} (x) = i^{-\nu} J_{\nu}(ix)$$
$$ K_{\nu} (x) = \frac{\pi}{2} i^{\nu +1} H_{\nu}^{(1)}(ix)$$
교재에 얘들의 limiting form도 적혀있는데 생략. x=0에서 I는 regular, K는 diverge하고, x=inf에서 I는 diverge, K는 regular하다는 사실 정도만 알아두면 된다.
3.11절(green ftn for cylindrical situation)에서 중요하게 등장하니 무시하면 안된다.
여기까지가 3.7절에서 등장하는 내용. 이 밑의 내용은 3.8절에서 등장.
11) 한켈 변환
8)에 나온 직교성 식의 연속화된 버전이다. 베셀함수는 다음의 orthogonality (in k)를 이룬다.
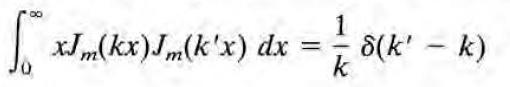
즉 0<x<inf에서 complete set을 이루고(사실 orthogonality랑 completeness는 상관이 없고, completeness relation을 보여야하지만 그냥 믿자-사실 아예 상관이 없진 않을텐데 수리물리 공부한 기억이 휘발돼서 잘 모르겠다. 아시는 분은 댓글 부탁드려요), 이를 기저로 하여 0<x<inf에 대해 정의되는 함수 A(x)를 다음과 같이 전개할 수 있다.

이를 한켈 변환이라고 하며, 푸리에-베셀 급수의 연속 버전이다.
즉 [cos sin 기저:푸리에급수=>푸리에변환]이라면 [베셀 기저: 푸리에-베셀 급수 => 한켈변환] 인 것.
더 알아보고 싶으면 다음의 링크 참고: 조금은 느리게 살자: 한켈 변환(Hankel Transform) (ghebook.blogspot.com)
12) spherical Bessel functions
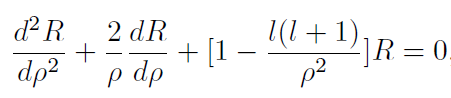
의 해. l(l+1)을 보면 눈치챌수도 있겠지만 양자역학에서도 나온다. 못봤다면 제대로 공부를 안한것..
그러나 잭슨에서는 다음의 맥락으로부터 나온다. 위에 적었던 베셀함수의 orthogonality (in k) condition에 다음과 같은 함수
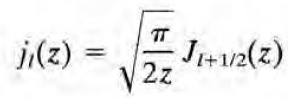
를 정의하여 대입하면
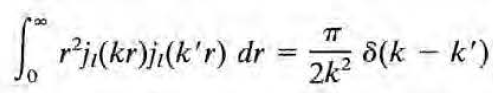
이 성립한다. 이는 j_l(kr)의 orthogonality condition이 된다. j_l(kr)은 completeness relation도 만족하는데, 그 식은 위 식을
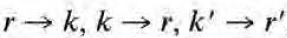
로 고친 식과 같다. 따라서 j_l(kr)은 complete set을 이루고, 이를 기저로 하여 함수를 전개할 수 있다.
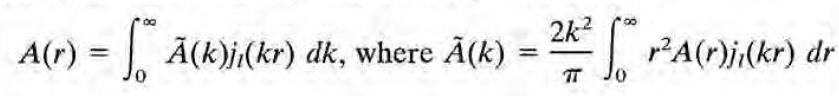
이러한 전개는 전자기학에서의 맥락에서는 전도성 매질에서 전류의 decay나, angular symmetry가 몇개의 l에 한정해서만 성립되는 상황으로 줄어들때의 시간의존성 자기확산을 다루는 경우를 다룰 때 등장하게 된다. 문제 5.35,36 참고. 그 외에도 9장 등 여러 곳에서 등장하고, 3장에서는 3.13절에서 잠깐 쓰인다.
베셀 함수와 마찬가지로, 구면 베셀함수 또한 구면 노이만 함수, 구면 한켈 함수 등등의 여러 버전이 존재한다. 궁금하다면 수리물리 책이나 다음의 pdf Spherical Bessel Functions (arxiv.org) 참고.
또한 베셀 함수에서와는 달리 닫힌 함수 꼴이 존재한다! (적어도 l이 작은 값일 때에 대해선)
3.7 Laplace Equation in Cylindrical Coordinates; Bessel Functions
원통좌표계에서 라플라스 방정식은 다음과 같다.
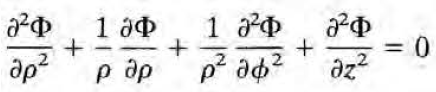
\( \Phi(\rho, \phi, z) = R(\rho) Q(\phi) Z(z) \) 로 변수분리하여 정리하면
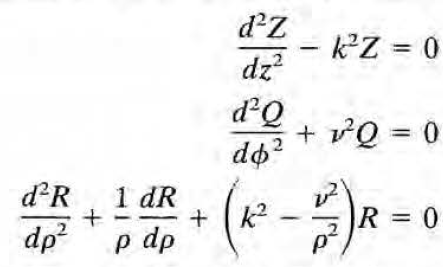
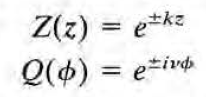
만약 관심영역이 전체 방위각을 포함한다면 \( Q(\phi) = Q(\phi + 2 \pi) \) 구속조건이 붙게 되고, \( \nu \)는 정수가 되어야 한다. 반면 k에는 그러한 구속조건이 없다. k는 나중에 경계조건에 의해 결정될 뿐이다. 일단은 양의 실수로 가정하자.
마지막 남은 R에 대한 미분방정식은 \( x= k\rho \)로 치환하여 정리하면 x에 대한 미분방정식으로 바뀌는데, 이 방정식이 바로 위에서 본 베셀방정식이 된다. 따라서 \( R(\rho) = J_{\nu} (k \rho) \)가 된다.
사소한 기호의 어뷰징이 있다. 변수가 바뀜에도 함수의 기호를 R로 그대로 쓴다는 점. 수식 전개에만 매몰되다보면 이것땜에 헷갈려서 변수 바꾸고 난뒤의 함수를 새로 \( \tilde{R} \) 같은 식으로 이름 붙이는 등의 삽질을 할 수 있는데 그냥 베셀 방정식에서 역으로 원래 방정식을 유도한다고 생각하면 편하다. 나만 이런 삽질을 했었을지도 모르겠지만... 가장 편한 방법은 사실 결과를 외우는것.
위의 10)이 튀어나온 배경에 대해 잠깐 언급할게 있다. 사실 라플라스 방정식의 변수분리 과정에서 k라는 상수를 정의할 때 k^2에 해당하는 부분을 -k^2으로 정의할 수도 있다. 이 경우 Z(z)가 \( e^{\pm ikz} \) (sinusodial function)가 되는 동시에, R에 대한 방정식도 바뀌게 된다. 이때 얻어지는 방정식이 바로 10)의 modified Bessel function이다.
3.8 Boundary- Value Problems in Cylindrical Coordinates
수식이 지저분하다는 것 빼고는 어려울게 단 하나도 없는 내용이 나오는 절이다.
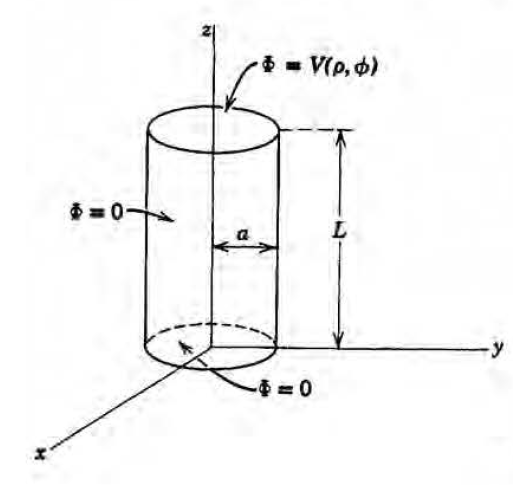
위 상황에 대한 라플라스 방정식을 원통좌표계에서 풀자.
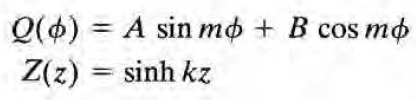
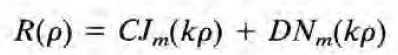
Q는 Q(phi) = Q(phi+2pi)로부터, Z는 z=0에서 Phi=0으로부터, R은 rho=a에서 Phi=0으로부터 나왔다. 이때 k는 다음과 같다.
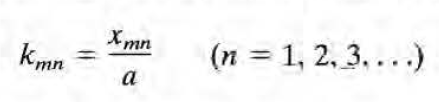
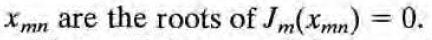
이 셋을 조합하면 다음과 같다. sum안의 식이 라플라스 방정식을 만족하므로 이들의 sum 또한 라플라스 방정식을 만족한다.
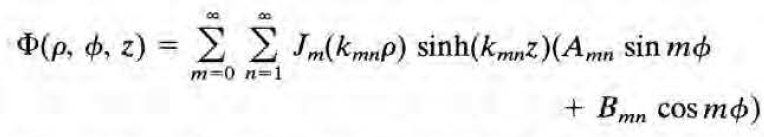
이제 z=L에서의 경계조건을 대입하면 다음을 얻는다.
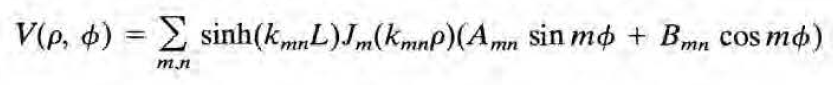
이로부터 Amn과 Bmn이 결정된다.
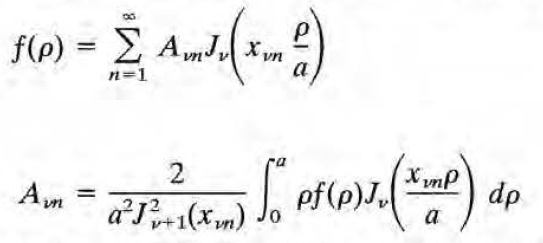
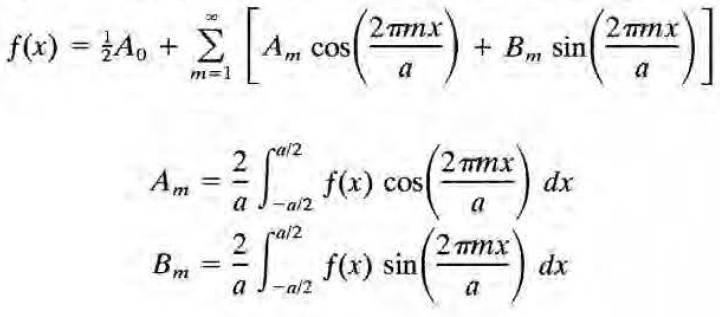
를 이용하여 결정할 수 있으며(왼쪽 거 먼저 그대로 적용->A_vn은 phi에 대한 함수로 나옴 -> 이를 오른쪽거의 f(x)로 취급->다만 적분 구간이 바뀌기 때문에 오른쪽거는 그대로 적용하진 못하고 그냥 직교성을 이용해 새로 보이는 게 낫다), 그 결과는 다음과 같다.
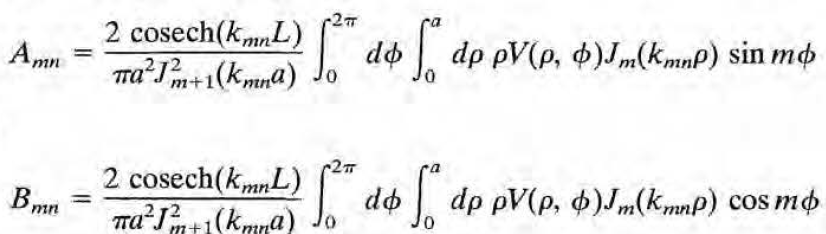
(단, 푸리에 급수에서 f(x) = (sum term) + 1/2 A_0 이었듯, m=0에 대해서는 1/2 B_0n을 사용해야한다)
그 뒤로는 다른 경계조건에 대해선 어떻게 풀어야 할지 간략히 다루는 내용들이 나온다. 위의 예시를 포함해 교재에 나오는 예시를 정리해보자면
(1) z=0 : 0 / rho=a : 0 / z=L : specified
위의 예시. radial part는 bessel, azimuthal part는 sin&cos, z part는 sinh
(2) z=0: 0 / rho=a: specified / z=L : 0
위아랫면이 0이고 옆면이 주어지는 경우. radial part는 modified bessel, azimuthal part는 sin&cos, z part는 sin
(3) z=0: specified / rho=inf : 0 / z=inf : 0
[맥락을 설명하자면 (1)의 경우에서 a->inf로 가는 경우(즉 open boundary)를 다루고 싶고, 식을 간단히 하고 싶어서 (z=0:0, z=L: specified)를 (z=L:0, z=0: specified)로 바꿨는데 z=L에서 0인 경우? 무한대에서 0되는 거랑 엮어볼까? 해서 L까지 inf로 보낸 것]
a->inf인 경우가 되어 k_mn이 discrete에서 continuous로 바뀜, sum_k도 int_k로 바뀜. 푸리에 급수에서 푸리에 변환이 된것과 동일하다. radial part는 bessel, azimuthal part는 sin&cos, z part는 exp(-kz)
이 경우의 일반식은 교재에서도 소개했는데 다음과 같다.
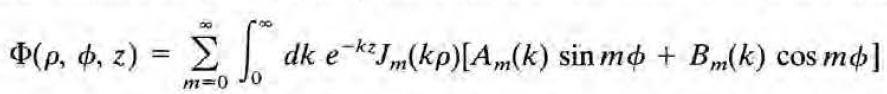
계수 Am(k)와 Bm(k)는 이 포스트 상단에서도 소개했던 다음의 공식(orthogonality in k)을 이용하여
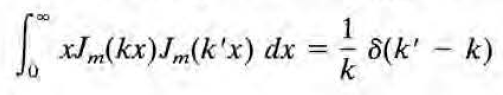
다음과 같이 결정된다. (이경우도 m=0일 땐 1/2 B_0(k)을 이용해야.- sin cos 항이 있어 한켈변환 뿐만 아니라 푸리에도 쓰기 때문)
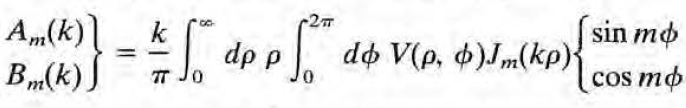
(추가 예시) 책에는 없지만 언급하면 좋을거 같아서..
z=0: / rho=a : 0 / z=inf : 0 -> (1)이나 (2)에서 specified=0을 대입하면 나옴. 결과는 \Phi = 0 .ㅋㅋ
z=0: / rho=a : specified / z=L : specified -> (1)과 (2)의 해를 중첩하면 나옴.
이 절에서 마지막으로 다루는 토픽은 구면 베셀 함수(spherical Bessel function)다. 뭔가 낯익더니만 양자역학에서 봤었더라. 자세한건 위에서 다뤘다.
3.11 Expansion of Green Functions in Cylindrical Coordinates
위 절에서는 cylindrical한 경계조건이 있는 라플라스 방정식을 풀었다. 그럼 cylindircal한 경계조건이 있는 푸아송 방정식(즉 내부에 전하가 존재하는 상황)을 풀려면 어떻게 해야할까? 바로 1장에서 봤던 그린함수를 이용하여 퍼텐셜을 구하는 방법을 이용해야한다.
그린함수를 구하기 위해 다음의 방정식과 델타함수의 표현으로부터 시작하자.
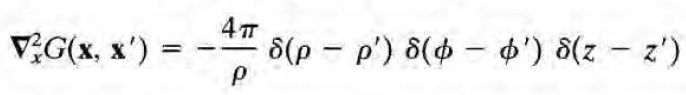
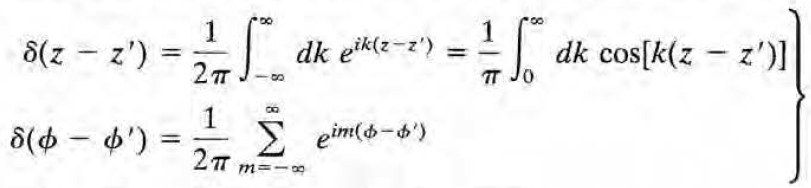
G를 다음과 같이 전개해보자. delta(z-z')을 전개한 기저(cos(k(z-z')) 및 delta(phi-phi')을 전개한 기저(exp(im(phi-phi'))와 같은 기저에서 전개했다고 생각하면 된다.
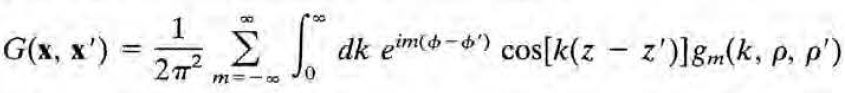
이를 방정식에 대입하면 다음을 얻는다.
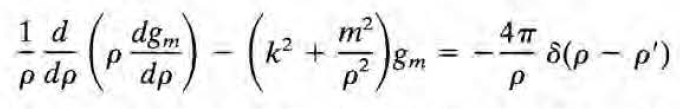
이제 이런 방정식은 너무 많이 풀어봤다. i) rho>rho'에서의 homo.DE 풀고 ii) rho<rho'에서의 homo.DE 풀고 iii) 두 해를 >,< 표기 이용한 곱 형태로 쓰고 iv) 디랙델타로부터 discontinuity 구해다 normalization factor(=식 전체 앞에 붙는 상수)를 결정하면 끝.
우선 좌변은 modified Bessel eqn이므로 rho!=rho'일 경우 I_m(k rho)와 K_m(k rho)의 선형결합이 해가 됨.
i)의 해를 \( \psi_1(k \rho ) \)로, ii)의 해를 \( \psi_2(k \rho ) \)로 두자.
iii)에서 g_m을 다음과 같이 둘 수 있다.
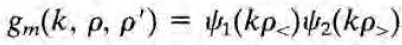
그린함수는 항상 rho<->rho' 대칭성을 만족시켜야 하기 때문. 어디선 psi1이고 어디선 psi2이면 전체 꼴은 반드시 psi1과 psi2를 모두 포함하는 꼴이어야 한다.
iv) 양변을 \( \rho=\rho'-\epsilon \) 에서 \( \rho=\rho'+\epsilon \) 까지 적분해 discontinuity 얻음
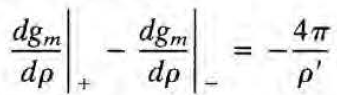
바로 위에서 만든 gm 식 대입
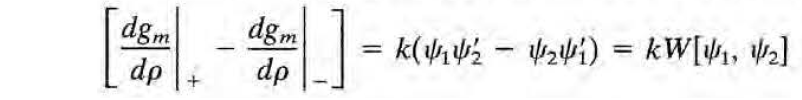
우변의 W는 Wronskian을 뜻함. 오랫만에 보는듯..
이제 수리물리에서 봤던 스트룸-리우빌 뭐시기가 뜬금없이 나오는데,
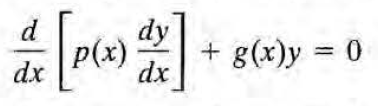
꼴의 방정식(이를 스트룸-리우빌 방정식이라 부름)에 대해 두 선형독립인 해의 wronskian이 1/p(x)가 됨을 이용하려고 얘기한 것이다. (아프켄 7.6.11번 문제 참고) 위의 \(g_m(\rho) \)에 대한 방정식은 양변에 \( \rho \)를 곱하고 보면 \( p(\rho )=\rho , g(\rho) = -\rho(k^2+m^2/\rho^2) \)인 스트룸-리우빌 방정식이라는 것을 볼 수 있을 것이다. 따라서
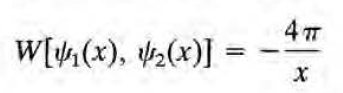

finite한 어떤 값이니 \( \psi_1 \)에 A라는 어떤 상수가 붙는건 이해가 간다. 그런데 \( \psi_2 \)의 K에는 왜 상수가 안붙느냐? 분명 자유도가 있을텐데. 라는 생각이 들 수 있는데, 조금만 기다려보라.

이고(앞전에 \(x=k \rho \)라고 정의했던걸 은근슬쩍 다시 집어넣었다), small x에서
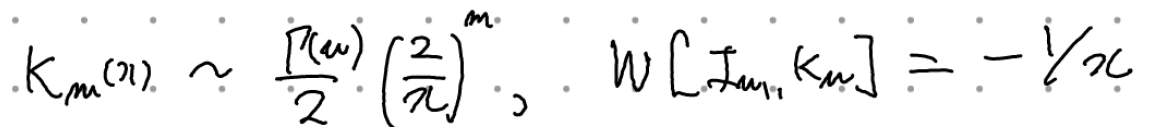
이므로 이를 위의 식에 대입하면 \( A= 4\pi \)로 결정할 수 있다. 따라서 임의의 \( \rho, \rho' \)에 대해 다음과 같이 \( g_m \)을 쓸 수 있다.
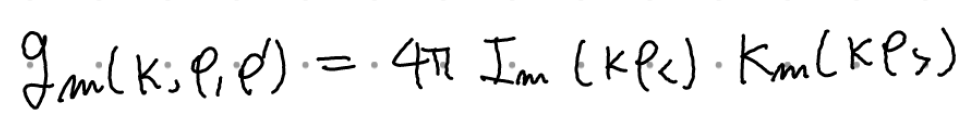
따라서 상수 B를 하나 더 정의해서 psi_2(k rho_>) = B K_m(k rho)라고 놓는다 치더라도 결국 AB=4pi가 되고 g_m 역시 동일하게 나온다. 왜 이런 착각을 했느냐/혹은 왜 이래도 되느냐 같은 의문을 가질 수 있는데, 계수의 자유도를 철저히 따져보기 위해 g_m의 식을 다음처럼 써보자.
$$ g_m(k, \rho, \rho') = A(I_m(k \rho_< ) +B K_m(k \rho_<)) (K_m(k \rho_> ) +C I_m(k \rho_>)) $$
(뒷 항에서 I_m+C K_m 이 아니라 K_m+C I_m으로 쓴건 rho->inf에서 I_m이 날라가고 K_m은 남는다는걸 미리 봤기에 이 케이스를 포함하면서도 계수의 자유도를 최대한 줄이려면 이처럼 표현하는 것이 좋기 때문)
즉 A,B,C 3개의 계수를 결정해야 한다. 그런데 우리는 rho=0, inf 에서의 경계조건 2개와 g_m의 discontinuity(곧 wronskian으로 정리되는) 조건 1개를 가지고 있다. 따라서 g_m이 유일하게 결정되는 것이다. psi1에 계수 A를, psi2에는 계수 1을 준 것도 이런 진단을 하고 나서, 계수의 자유도가 차지도 부족하지도 않으면서 최종적으로 gm을 결정하는데 있어서도 문제가 없게끔 하는 선택지 중 하나를 임의로 고른 것이다. 이걸 일일히 본문에서 설명하기엔 너무 잡스러운 이야기라 생략한 듯 싶다. 더 심한 것들도 생략하는데 뭐..
지금 푼 gm은 boundary가 없을 때를 상정한 것이므로 전체 그린함수 G(x,x')는 1/|x-x'|이어야 한다. 따라서 다음이 보여졌다.
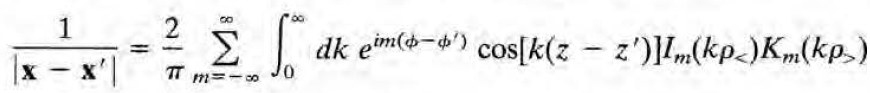
잭슨은 굳이 다음의 식까지 써줬다. 실함수로만 나타내도록 정리하겠다면서.. (m의 범위가 양수로 줄어들고 exp(imphi->cos(m phi)가 된 것을 확인해라)
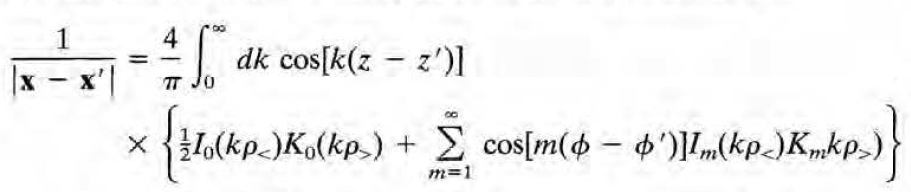
이것이 이번 절의 핵심 결과이다.
덧붙여 한가지 자잘한(?) 공식을 유도한다.
위 공식에서 x'->0으로 보내면 m=0 항만 살아남는다. rho_< ->0, rho_> = rho가 되고, small x에서 I_m(x) ~x^m이기 때문. (K_m(k rho>)=K_m(k rho)= finite)
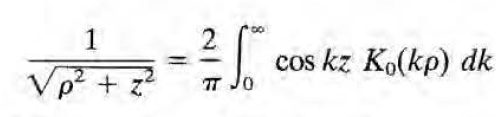
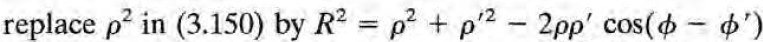
를 하면, 좌변은
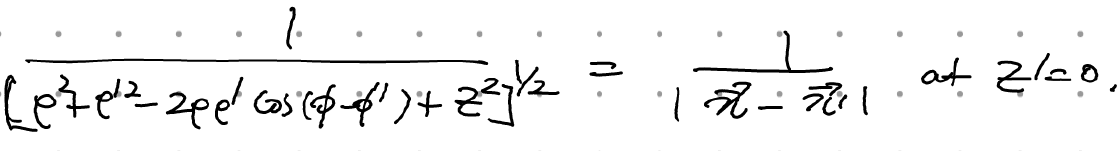
((z-z')^2 = z^2 at z'=0이므로)
우변은
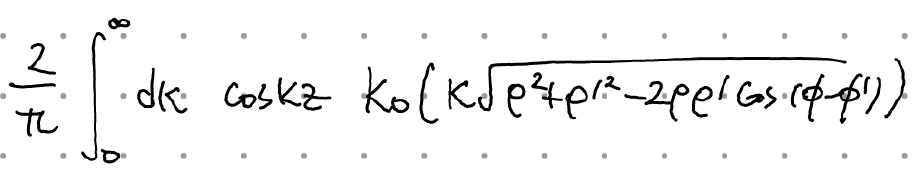
가 된다. 이를 위에서 구했던 1/|x-x'|과 비교하면
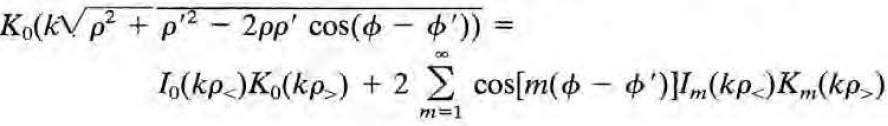
이 성립해야한다.
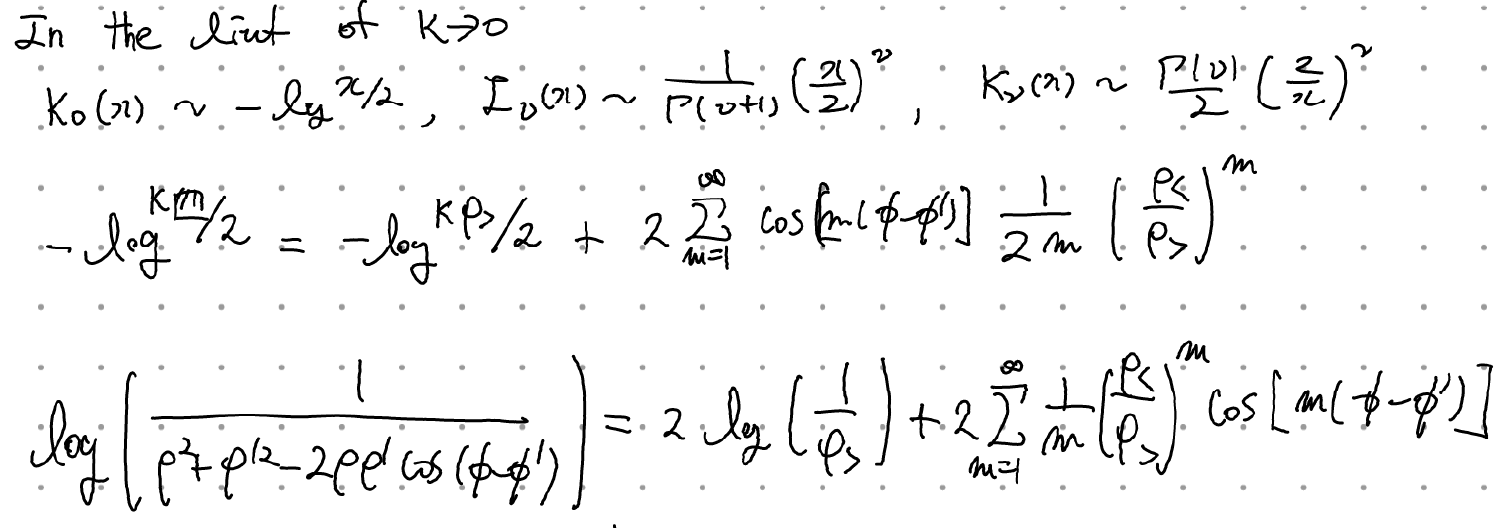
따라서 위와 같은 공식을 얻을 수 있으며, 이는 2차원 free space에서의 푸아송 방정식의 그린함수이다. 3차원 free space에서의 푸아송 방정식의 그린함수인 1/|x-x'|의 expansion으로부터 이를 유도해냈다는 의의가 있다. 물리적으로는, z'=0으로 두고 k->0을 취했다는 것은 z축 방향으로의 퍼텐셜 변화를 없앴다는 것으로, 3d에서 원점에 있던 점전하를 z축에 놓인 선전하로 길게 늘인 상황과도 같다. 구체적인 설명은 다음의 PSE 링크 참고. electromagnetism - Jackson's derivation for 2D Green's function from 3D Green's function - Physics Stack Exchange
또한 이 식은 문제 2.17번에서와 같이 다른 방법으로도 유도할 수 있다. (사실 소문제 1번 논리가 영 납득이 안되는데 누가 설명해주실분..)
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 4.1 (0) | 2024.10.11 |
|---|---|
| [잭슨 전자기학] Ch3 - (4/4) (0) | 2024.10.05 |
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |
| [잭슨 전자기학] Ch2 (0) | 2024.09.30 |