2.1 Method of Image

z>0는 실제 전하가 있는 공간(=부피 내), z=0은 경계, Phi(z=0)=0은 경계조건(디리클레 조건), z<0은 전하가 없는 공간(=부피 밖)
z>0의 퍼텐셜 = 실제 전하가 만드는 퍼텐셜 + 가상전하가 만드는 퍼텐셜
z<0의 퍼텐셜 = 부피 밖이므로 0 (이전 글 ch1-후반부 참고)
2.2 ~ 2.5 까진 여러 예시에 대해 영상법을 적용해보는 내용. 부피 내에 점전하가 하나 있고, 다양한 모양의 표면을 준다.
퍼텐셜을 구하고, surface에 대전되는 면전하를 구하고, 그 면전하로부터 전하가 받는 힘을 구해본다.
공통된 과정은 다음과 같다.
(1) 가상전하가 있을 만한 곳을 직관적으로 찍고, 그 위치와 전하량을 변수로 둔다.
(2) 실제 점전하와 가상전하 둘이 만드는 퍼텐셜을 구하고, 그 퍼텐셜이 주어진 표면에서 0이 되어야 한다는 조건(접지)으로부터 가상전하와 전하량을 구한다.
(3) 면전하는 다음의 공식을 통해 구한다.
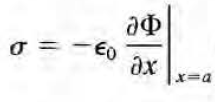
(4) 표면의 면전하가 실제 점전하에 가하는 힘은 2가지 방법으로 구할수 있다.
한 가지는 가상전하가 점전하에 가하는 힘으로 구하는 방법이다. 두 점전하 간 쿨롱 힘만 구하면 되니 엄청 쉬운 방법.
다른 하나는 미소 면전하마다 점전하에 가하는 힘을 구해 적분하는 방법이다.
2.2 Point Charge in the Presence of a Grounded Conducting Sphere

접지된 도체구 밖에 실제 점전하가 있는 상황.
잭슨에도 나오고 그리피스에도 나오는 유명한 예시. 생략.
2.3 Point Change in the Presence of a Charged, Insulated, Conducting Sphere
여기서 말하는 charged insulated conducting sphere란 대전된 도체구인데 접지가 되어있지 않다는 뜻이다. 다른곳과 연결되어 있지 않아 insulated 되었다는 뜻이지, 부도체(insulator)란 건 아니다.
아이디어: 일단 접지시킨다. 그럼 구 밖 전하 q에 대해 구 내에 가상전하 q'을 잡을수 있고, 접지된 곳으로부터 q'만큼의 전하량이 구로 흘러들어와 표면에 퍼진다. 이제 접지를 끊고, Q-q' 만큼의 전하량을 추가로 구에 공급해준다. 그러면 외부전하 q와 가상전하 q'이 이미 평형을 이루고 있었으므로 Q-q'의 추가 전하는 표면에 고르게(마치 q와 q'이 없었을 때마냥) 퍼진다.
외부 전하가 구 근처에 위치하면 특이한 일이 벌어질수도 있다. 가령 q도 Q도 양수인데 attractive force가 작용할수도 있다. 자세한건 잭슨에.
2.4 Point Charge Near a Conducting Sphere at Fixed Potential
2.2 상황에서 구 표면 전위가 0이 아니라 V로 바뀐것
구 가운데에 표면 위치의 전위가 0이 되도록 하는 가상전하 하나만 더 추가하면 끝.
2.5 Conducting Sphere in a Uniform Electric Field by Method of Images
아이디어)
평행한 전기장을 z=inf 와 z=-inf 에 각각 -Q와 +Q의 전하량을 가진 전하를 두어 +z방향의 전기장을 모사한다.
구 내에 가상전하 2개를 두게 된다. (각 전하마다 가상전하 1개씩. 전하-가상전하 한쌍씩 차례대로 넣는다 생각하면 표면의 전위는 그대로 0이다)

그래서 실제 점전하 2개와 가상전하 2개, 총 4개의 전하가 만드는 퍼텐셜의 합으로 도체구 밖의 퍼텐셜을 구할 수 있다.
구가 도체이므로 표면은 등전위고, 구한 도체구 밖 퍼텐셜에 대입해보면 0이 나온다. 도체 내부 전기장은 0이므로, 도체구 내 퍼텐셜은 전부 0. 이는 경계조건 밖(=전하가 없는 공간)의 퍼텐셜과 전기장이 0인것과도 일치.
insulated sphere로 해도 동일한 결과 얻는다 함.
2.6 Green Function for the Sphere; General Solution for the Potential
어찌보면 2장의 본격적 시작. 이전까지는 학부 범위라고 봐도 되니까.

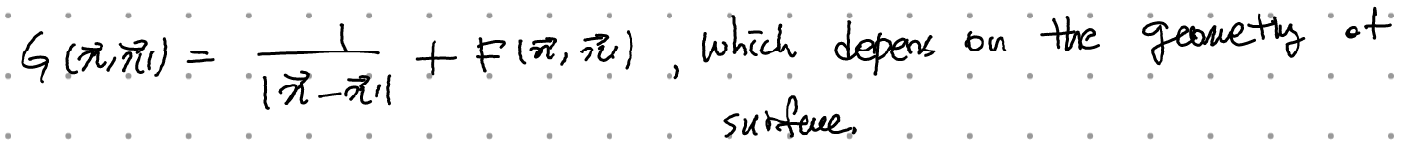
디리클레 조건이 주어질 경우 구 표면에서 G=0임을 ch1 후반부에서 보았다. 즉 우리가 풀 문제는 표면에서 G=0이 되도록 하는 적절한 F가 존재할 것이라 믿고 G를 구하는 것이다. 그리고 이는 영상법을 통해 쉽게 구해진다. (전하량을 4pi eps0으로 둔다)

구면좌표계로 옮기면(이라고 잭슨은 표현하는데 굳이 그렇게 생각하지 않아도 되긴 한다) 다음과 같다.

사소한 언급: x<->x' interchangablity 확인 가능. x'=a에서 0이 됨. 마찬가지로 x=a를 넣어도 0이 됨.
디리클레 조건하에서 푸아송 방정식의 해는 다음과 같았다.

첫항은 그냥 계산하면 되고(문제에 주어진 rho와 바로 위에 써논 G를 이용하여), 뒷 항을 계산해야하는데 이때 dG/dn'을 계산해야한다. 이 때 n'은 우리가 관심있는 영역(지금껏 어물쩍 '부피'라고 언급해온, 전하가 실제로 존재하는 영역)에서 표면 바깥으로 향하는 방향이다. 즉, 구 바깥에서 내부로 향하는 방향이다.
즉 다음이 성립한다 ( x'은 실제 점전하의 위치벡터 방향, 즉 원점에서 구 밖으로 향하는 radial 방향)


따라서 위의 푸아송 방정식의 해의 뒷항(=라플라스 방정식의 해)은 다음과 같다. 물론 x는 구 바깥의 점이다. (안쪽이면 관심 영역밖, 0)

여기서

이고, 입체각 dOmega'은 그냥 구 중심에서 표면의 점 (a, theta' , phi' ) 근처 미소영역이 차지하는 입체각이므로 sin theta' d thtea' d phi'과 같다.
만약 전하가 구 밖이 아니라 안에 있다면(interior case), 달라지는 유일한 건 관심 영역이 구 밖이 아니라 구 안이 되어 n'의 방향이 x'의 방향과 같아진다는 것이다. (라플라스 방정식에는 전하가 없지 않나요 - 그냥 관심영역(방정식을 풀 영역)을 구 안으로 설정했다 치면 됨)따라서 위의 라플라스 방정식의 해의 분자를 (x^2-a^2)에서 (a^2-x^2)로 고쳐주기만(=부호만 바꿔주기만) 하면 된다.
2.7 Conducting Sphere with Hemispheres at Different Potentials

도체 구를 반 갈라서 위는 +V, 아래는 -V가 되도록 한 상황. 가운데에 작은 부도체 ring을 끼워놓았다는 설정이다. (사실 여기서 '도체'라는 조건은 쓰이지 않는다. 이런 상황을 어떻게 만드느냐(현실성이 있느냐)를 설명하기 위해 도체 반구 2개를 준비하고 각각에 전압을 걸어주면 면의 퍼텐셜이 uniform하게 만들어질 수 있으니 도체를 언급한 것)
2.6에서의 라플라스 방정식의 해를 이용하여 다음과 같이 퍼텐셜을 구할 수 있다.
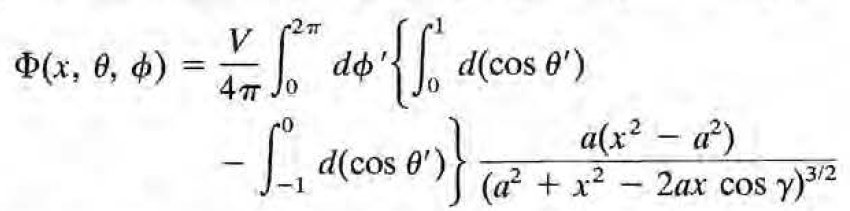
뒷항의 (-) 부호는 아래쪽 반구의 퍼텐셜이 -V이기 때문.
d(cos theta) 라는 표기가 익숙치 않은 사람을 위해 설명하면 d (cos theta) = - sin theta d theta이다. 치환적분을 하는데 변수를 따로 정의하기 싫을 때 쓰는 표기라고 생각하면 된다. 구간은 cos theta의 값의 범위로 설정. 즉
int 0 to 1 d (cos theta) = int pi/2 to 0 -sin theta d theta = int 0 to pi/2 sin theta d theta (상반구에 해당)
int -1 to 0 d (cos theta) = int pi to pi/2 -sin theta d theta = int pi/2 to pi sin theta d theta (하반구에 해당)
이다.
cos gamma의 식이 더러운데다 분모에 있어서 위 적분의 closed form은 존재하지 않는다. 그래서 z축 위라는 특별한 경우에 한해서만 계산해보자.

다시 general한 식으로 돌아가서, 잠깐 다음처럼 정리해보자.

그럼 general한 식은 다음과 같이 쓸 수 있다.

이제 괄호 안의 식을 x>>a, 즉 alpha <<1에서 전개해보도록 하겠다.

그럼 일반적인 식은 최종적으로 다음과 같이 정리 가능하다.

(언뜻 쉽게 넘어갈 수 있는 부분인데, (2.25) 식을 직접 보이려면 상당히 고되다. [전자기학] 잭슨의 광기 (2.25 식 증명) (tistory.com))
전체 퍼텐셜이 theta에 대한 odd function으로 나타나야 하므로, cos theta의 홀수제곱항만 나타나는 것을 확인할 수 있다. 잭슨에 언급된 symmetry란 건 이것을 말한다.
그러나 여기서 더 중요한 통찰은 따로 있다. alpha의 거듭제곱항으로 전개하는게 아니라, a/x의 거듭제곱항에 대해 전개해보자.

르장드르 다항식이 등장한다! ...사실 수리물리나 양자역학에서 마주쳤을 내용이기에 놀랍게 들리진 않을것이다.
3장에서 대칭성이 존재할 때 (정확히는 3.3의 원통대칭성)의 boundary value problem을 풀게될텐데 르장드르 다항식을 다시 보게 될 것이다.
2.8 Orthogonal Functions and Expansions
수리물리 때 마르고 닳도록 했던 내용. 생략.
2.9 Separation of Variables; Laplace Equation in Rectangular Coordinates
직육면체 경계주고 윗면 하나 빼곤 다 퍼텐셜 0으로 주고 윗면 퍼텐셜만 V(x,y)로 주는 상황(디리클레 조건). 그럼 중첩원리로 6면의 퍼텐셜이 다 임의의 값인 경우에 대해서도 풀 수 있게 된다.
그리피스 때 지겹도록 했던 변수분리... 생략.
2.10 .A Two-Dimensional Potential Problem; Summation of a Fourier Series
2D 직교좌표계 변수분리.. 생략.
교재에서 어떤 상황에 대해서 이걸 푸는데, 푸리에 급수로 구해진 해가 희한하게 closed form으로 정리되는 케이스여서 구경해볼만 하다.
2.11 Fields and Charge Densities in Two-Dimensional Corners and Along Edges
2차원 polar coordinate에서 경계조건과 함께 라플라스 방정식을 푼다.
아주 익숙한 논리가 펼쳐질 거라 생략해도 무방하긴 한데 한번 써본다.
라플라스 방정식은 다음과 같다.

변수 분리 쓰고 상수 nu를 다음과 같이 정의한다.

그럼 해는 이렇게 나온다.

nu=0일 때는 특수한 경우로 해가 다음과 같다.

가장 일반적인 해를 쓰려면 이들의 선형조합으로 일반해를 쓰면 된다. (잭슨에 써있진 않음)
만약 관심영역이 0<= phi <=2pi 전체를 커버한다면, Psi(phi)가 구속조건 Psi(phi)=Psi(phi+ 2pi)를 만족시켜야 퍼텐셜이 한 점에서 유일하게 결정될 수 있으므로, 이 구속조건으로부터 B0=0 및 nu는 정수여야 한다는 조건이 붙는다. nu가 음의 정수일 때의 식은 양의 정수일 때의 식에서 계수만 바꾼 꼴이므로, 선형독립적인 것들만 추리면 nu는 0 또는 양의 정수로 제한 가능하다. 따라서 이들의 선형 조합으로 일반해를 다음과 같이 쓸 수 있다.

rho=0일 때 발산하는 term들이 존재한다. 즉 문제의 관심 영역이 원점을 포함하고, 전하가 존재하지 않으면(점전하가 퍼텐셜에 singularity를 주는 것을 생각하라)이런 term들의 계수(즉 b_n)들은 0이 되어야 한다.
이제 교과서에서 풀고자 하는 상황을 보자.

위 상황에 대한 구체적 설명 및 일반해에 경계조건을 적용한 식은 다음과 같다.

nu가 정수가 아닌 이유는 관심영역이 전체 phi를 전부 커버하지 않기 때문에 구속조건이 풀린것.
아직 계수 a_m들이 정해지지 않았는데, 이는 rho -> inf 에서의 퍼텐셜이 어떻게 정해지느냐에 따라 unique하게 결정된다. 사실 우리가 지금까지 본 경계는 open boundary였다. closed boundary에 대한 condition을 주기 위해선 무한대 거리에서의 퍼텐셜도 정해줘야 boundary가 closed될 수 있는 것이다. (혹시나 해서 말하자면 0<=phi<=beta는 계속 깔고 말하고 있는 중)
혹시나 전하분포를 아직 지정하지 않아서라고 생각했을 수도 있는데, 우리가 풀고 있는 방정식이 라플라스 방정식이었음을 상기하라.
rho ~ 0 에 대해서만 구체적으로 몇가지 물리량들을 계산해보자. 우선 퍼텐셜은 다음과 같다. (a_1이 nonzero라고 가정: 이를 remote boundary condition이라고 부르는 듯하다. 만약 대칭성 같은게 개입해 a1=0으로 만들어버릴 수도 있긴 하다고 하는데 뭐 그땐 그때가서 따로 생각해주면 되니 어렵지는 않다)

전기장은 다음과 같다.

면전하밀도는 다음과 같다. phi=0에서든 beta에서든 rho~0에서는 면전하밀도가 동일하다.

여기서 뒤의 지수항에 주목하자. beta < pi 이면, rho ~0에서 면전하밀도도 ~0이라는 것이다. 즉 전하가 쌓이지 않는다. 반면 beta>pi이면 rho~0에서 면전하밀도는 발산한다. 도체에서 뾰족한 쪽의 전하밀도가 높다고 하는 이야기를 들어봤을텐데, 이 이야기를 재확인할 수 있는 사례이다.
구체적인 몇가지 각도에 대해 원점 근처 면전하밀도의 거동을 구해보면 다음과 같다.

2.12 Introduction to Finite Element Analysis/or Electrostatics
수치계산 테크닉적인 내용. 생략.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
|---|---|
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |
| [잭슨 전자기학] Ch1 - (2/2): 푸아송 방정식, 라플라스 방정식, 그린함수, 경계조건 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (1/2): 전기장, 전위, 가우스법칙, 쌍극자층 (0) | 2024.09.29 |
| 잭슨 전자기학 정리 (0) | 2024.09.29 |