1.1 쿨롱 법칙에 대한 정성적 설명.
역제곱법칙, 전하의 부호, vector sum을 해야한다는 등.
1.2 전기장 및 디랙-델타 함수에 대한 설명.
전기장을 간단하게 F=qE로부터 유도한다. 즉 단위전하 당 힘으로 바라본 것.
보편적인 방식인 discrete -> continuous case로 일반적인 공식을 유도.

$$ \vec{E}(\vec{x}) = \frac{1}{4 \pi \epsilon_0} \int \rho(\vec{x}') \frac{\vec{x}-\vec{x}'}{|\vec{x}-\vec{x}'|^3} d^3 x' $$
대충 discrete한 전하 q를 continuous한 전하 분포 \(\int \rho(x') d^3 x'\) 로 바꾼 것이라고 보면 된다.
디랙-델타 함수 성질 7개가 언급되는데 다 쉬우니 생략.
discrete한 전하분포가 만드는 전기장을 위의 continuous한 공식을 이용하여 구하려면 rho(x)를 다음과 같이 두면 된다.

1.3 가우스 법칙 (Gauss's Law)

유도과정은 다음과 같다.

위와 같이 점전하 q가 분포한다고 생각하자.
미소 면적을 통과하는 전기장의 flux는 다음과 같이 구해진다.

이 때 면적의 법선벡터 n과 전기장 E가 이루는 각 theta과 전하 q로부터의 입체각 Omega 사이에 다음의 관계가 성립한다.

da cos theta : da를 da와 q를 이은 선분과 수직이 되도록 정사영한 넓이
따라서

따라서 적분하면

q가 부피 V 내부에 있냐 외부에 있냐 따라서 갈리게 되는 이유: q가 V 외부에 있을 때는 위의 그림에서 n과 E가 이루는 방향이 반대가 되는 경우가 있어 점선과 S의 교점 두 곳에서의 E dot n da 값이 상쇄되기 때문.
따라서 단일 점전하 q에 대한 가우스 법칙을 유도했고, 이제 이걸 여러개의 점전하로 확장하고(discrete case), 이를 다시 연속적인 공간전하분포로 확장하면 처음의 가우스법칙에 대한 유도를 완료할 수 있다.
1.4 가우스 법칙의 미분형 (Differential form of Gauss's law)

유도는 1.3의 식을 발산 정리를 이용하여 좌변을 정리해내고 한 변으로 넘겨서 적분 기호 내의 식이 0이 됨을 이용하여 보임. (임의의 부피 V에 대해 성립해야하므로)
1.5 스칼라 퍼텐셜 (scalar potential)
연속전하분포에 대한 전기장은 다음과 같았다.

이 때 다음이 성립하므로,

(유도는 x-x'을 r로 치환해서 보이면 편하다. 원점을 어디다 두느냐 문제로 인해 좀 꺼려질수도 있는데, 우변의 gradient는 x 좌표계 기준(대충 x'이 아니라 x로 미분한다는 뜻)이라 x'을 상수취급할 수 있고 따라서 r로 치환해도 문제 없다. 애초에 gradient를 어떻게 계산하는지 모르겠다...면 vector derivative of r^n (tistory.com) 참고)
전기장은 다음과 같이 고쳐쓸 수 있다.

따라서 다음의 스칼라장 (scalar field)을 정의하면
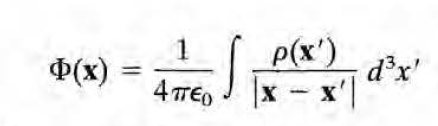
전기장을 다음과 같이 쓸 수 있다.

이 때의 Phi(x)를 스칼라 퍼텐셜(scalar potential) 또는 전위라고 한다.
이로부터 두가지를 알 수 있다.
(1) (scalar field의) gradient의 curl은 0이므로, 전기장의 curl은 0이다.
(1-1) 특정 vector field의 divergence와 curl을 알면 전체 공간에서 vector field의 값을 결정할 수 있다. (사실 유일하게 결정할 수 있는건 아니고 laplace eqn을 만족시키는 scalar function의 gradient 만큼의 차이는 존재 가능하다 (up to ~~) ) 지금까지는 전기장의 식을 이용해 가우스 법칙을 유도하여 전기장의 divergence를 구할 수 있었고, curl이 0임을 구했으나, divergence와 curl로부터 역으로 전기장의 식을 다시 구해낼 수도 있다는 얘기다.
(2) 전기력이 한 일
전체 공간에 전기장이 퍼져있고 그 가운데 점전하 q가 존재하고 있을 때, 그 전하가 받는 힘은 다음과 같았다. (즉 장이 전하에 가하는 힘)

그럼 점 A에서 점 B로 전하를 움직이는데 드는 일은 다음과 같다. (즉 장이 전하에 가하는 힘을 극복하고 움직이는데 드는 총 에너지)


이는 두 점 사이를 이동하는데 드는 일이 이동 경로에 의존하지 않는다는 점을 시사하며, 전기력이 보존력(conservative force)임을 말해준다. 사실, 보존력은 항상 위와 같은 방식으로 퍼텐셜 에너지가 잘 정의된다.
(2-1) 만약 점 A에서 출발해 다시 A로 돌아오는 경로(즉 closed loop)로 전하를 움직이는 경우, 들어가는 일은 위 공식에 따라 0이다.
이는 스토크스 정리로부터도 보일 수 있는 부분이다.
1.6 면전하분포와 면쌍극자분포(쌍극자층) / 전기장과 전위의 불연속성

이런 식으로 면전하가 존재한다고 하자. 면 밑에는 전기장 E1이, 위에는 전기장 E2가 있고, 밑에서 위로 향하는 방향으로의 법선벡터 n을 정의하면
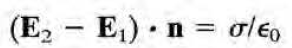
위의 식이 성립한다. 이것이 의미하는 바는 "면전하가 존재한다면 전기장에 discontinuity가 생긴다"는 것이다.
구체적으로, normal(면에 수직인) 방향으로는 sigma/eps0만큼, tangential(면에 평행한) 방향으로는 0만큼 존재한다.
유도) normal 방향에 대해서는 점선으로 표시한것처럼 작은 면적에 대해 매우 얇은 가우스면(직육면체로 두면 편함)을 잡아 가우스법칙을 써서 보일 수 있다. tangential 방향에 대해서는 위의 가우스면의 옆면(직사각형)에 대해 경계를 따라 선적분을 하여 보일 수 있다.
이 식은 이후 경계값문제(boundary problem)을 풀 때 계속해서 쓰이게 될 것이다.
면전하가 만드는 퍼텐셜은 다음과 같이 쓸 수 있다.
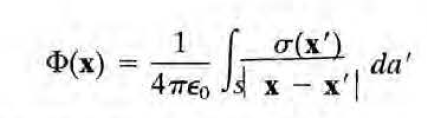
점전하나 부피전하의 퍼텐셜과도 사실상 거의 동일하다. (전하가 들어가는 부분만 다른데, \(q~ \rho dV ~ \sigma da \)인 셈을 생각하면 거의 동일) 면전하가 만드는 퍼텐셜은 전기장에서와는 달리 연속적이다.
"퍼텐셜이 불연속적"인 경우가 있을까? 있다.
퍼텐셜이 연속인 경우: 공간전하, 면전하
퍼텐셜이 불연속인 경우: 점전하(전하 위치에서 불연속), 선전하, 쌍극자층(dipole layer)
쌍극자층에 대해 알아보자. 크기가 같고 부호가 다른 두 면전하가 매우 가까이 붙어있는 형태다.
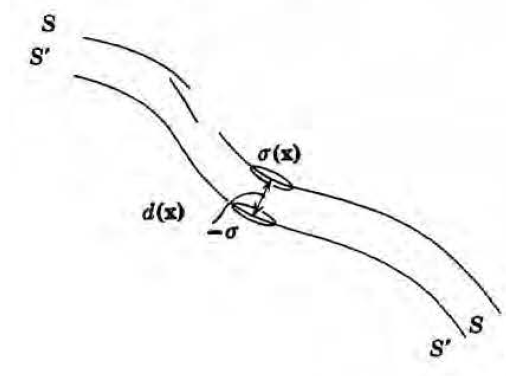
이 쌍극자층의 strength D(x)는 다음과 같이 정의된다.
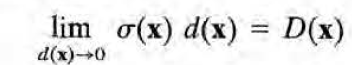
이 때 dipole moment의 방향은 (-)전하에서 (+)전하로, 면에 수직인 방향으로 정해진다. (면이 휘어져있으면 당연히 방향은 x에 의존)
이 쌍극자층의 퍼텐셜을 구해보자. 단순히 두 면전하의 퍼텐셜을 합하면 된다(superposition principle)
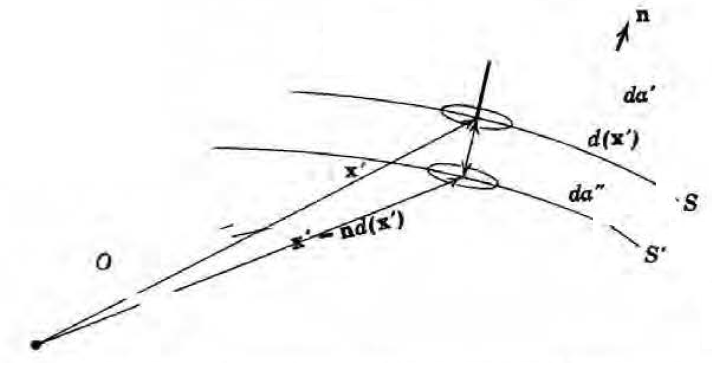
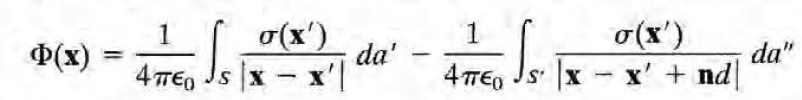
다음의 (3차원에서의) 테일러 전개를 이용하자.
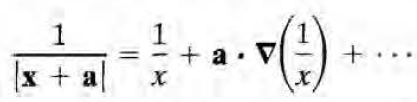
$$ \frac{1}{|\vec{x}- \vec{x}' + \hat{n}d |} = \frac{1}{ |\vec{x}- \vec{x}'|} + \hat{n} d \cdot \nabla \left( \frac{1}{|\vec{x}- \vec{x}'|} \right) = \frac{1}{|\vec{x}- \vec{x}'|} - \hat{n} d \cdot \nabla ' \left( \frac{1}{|\vec{x}- \vec{x}'|}\right) $$
(gradient를 x 좌표계가 아닌 x' 좌표계에서 하는 걸로 바꿈에 따라 \( \nabla -> \nabla ' \) 이 되었고 부호도 바뀌었다.)
즉 d->0에서 위의 퍼텐셜은 다음과 같이 정리된다.
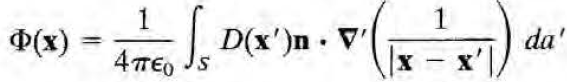
(참고로, 위 식의 integrand는 dipole moment가 \(\vec{p} = \vec{n} D da' \)인 쌍극자가 만드는 퍼텐셜 \(\vec{p} dot \vec{x-x'}/ 4\pi \epsilon_0 |x-x'|^3\)과 동일하다. 즉 이는 쌍극자층의 퍼텐셜을 유도하는 또다른 방식이기도 하다.)
위에서 가우스 법칙을 유도할 때 썼던 동일한 테크닉을 적용하여 integrand를 단순화할 수 있다.
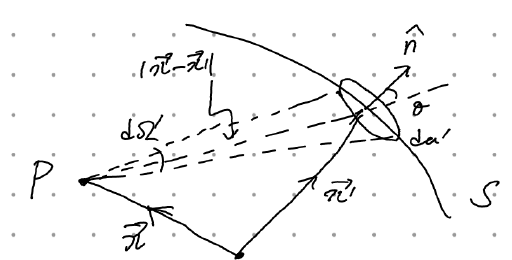
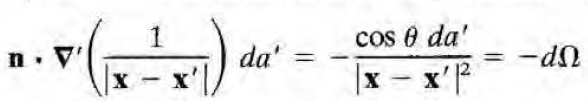
$$ \mathbf{n} \cdot \nabla ' \left( \frac{1}{|\vec{x} - \vec{x}'|} \right) da' = - \frac{ \cos{\theta} da'}{ | \vec{x} - \vec{x}' |^2} = - d \Omega $$
잠깐 부호를 짚고 넘어가자면, 두번째 등호는 딱히 어려울게 없고(가우스법칙 논의때와 정확히 동일), 첫번째 등호가 gradient에 prime이 있어서 부호가 헷갈릴 수도 있는데 그냥 분모에 절댓값이 있으므로 x'-x로 바꿔놓고 하면 된다. 그럼 \( - (\vec{x}' - \vec{x} ) / |\vec{x}'-\vec{x}|^3 \) 이 나올테고, \( n \cdot (\vec{x}'- \vec{x}) = \cos{\theta} |\vec{x}'-\vec{x}| \)이므로 첫번째 등호가 성립한다. \( \vec{x}' - \vec{x} \) 의 방향이 P에서 da'으로 가는 방향과 반대임을 생각할것.
따라서 쌍극자층이 만드는 퍼텐셜은 다음과 같이 깔끔하게 정리된다.
$$ \Phi(x) = - \frac{1}{4 \pi \epsilon_0} \int_S D(x') d\Omega $$
D(x')이 상수라면 적분 기호 밖으로 꺼낼수 있고, 위치 x에서의 퍼텐셜은 x에서 쌍극자층을 바라봤을때 차지하는 총 입체각에 비례하게 된다. 이를 이용하여 쌍극자층의 퍼텐셜에 있는 불연속성을 간단한 논의를 통해 확인할 수 있다.
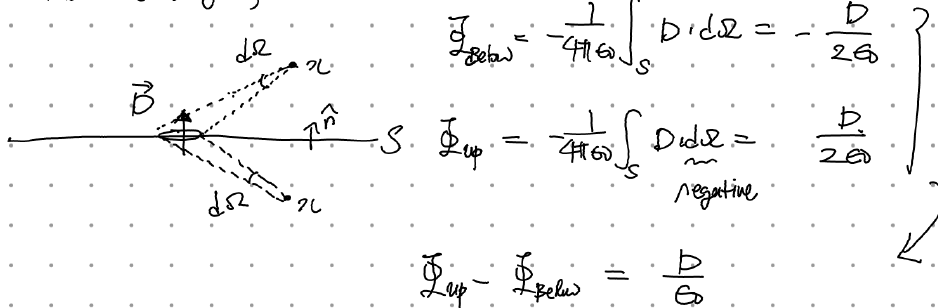
수식적으로는 쌍극자층 위아래에 따라 입체각 \(d\Omega\)의 부호가 바뀌기 때문이다. (\(d\Omega\)의 부호는 법선벡터(=D와 평행=(-)전하에서 (+)전하로 향하는 방향)와 \(\vec(x')-\vec(x)\)를 내적한 것과 같음을 상기)
이러한 퍼텐셜의 불연속성은 쌍극자가 만드는 퍼텐셜이 원점에서 디랙-델타 함수에 의한 발산 항을 가지고 있기 때문이다. 쌍극자층이 만드는 퍼텐셜은 무수히 많은 쌍극자들이 만드는 퍼텐셜의 합(=적분)을 통해서 구해질 수 있고, 따라서 디랙-델타 함수가 적분되며 유한한 값을 지니고 나타나게 되는데 이것이 퍼텐셜의 discontinuity이다. 4장에서 다시 보게 될 것( [잭슨 전자기학] Ch 4.1).
$$ \Phi_{dipole} = \frac{1}{4 \pi \epsilon_0} \frac{\vec{p} \cdot \vec{r}}{r^3} - \frac{\vec{p}}{3\epsilon_0} \delta(r) $$
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
|---|---|
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |
| [잭슨 전자기학] Ch2 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (2/2): 푸아송 방정식, 라플라스 방정식, 그린함수, 경계조건 (0) | 2024.09.30 |
| 잭슨 전자기학 정리 (0) | 2024.09.29 |