1.7 Poisson and Laplace Equation
두 방정식 다 퍼텐셜을 구하는 방정식이다. (정확히는 정전기적 퍼텐셜)

를 가우스 법칙에 대입하여 얻은

를 푸아송 방정식(Poisson Equation)이라고 한다.
이 중 특수한 경우로, 공간전하분포가 없는("charge-free region"), 즉 rho=0인 case에 대한 방정식은

와 같으며 이를 라플라스 방정식(Laplace Equation)이라고 한다.
전하 분포가 없더라도 전위가 존재할 수 있느냐?
우선 수식적으로는 아래에서 다루겠지만, (적절한) 경계조건이 주어지면 그에 의해 강제로 전위가 결정되어 존재하게 된다.
물리적으로는, 어떤 경계가 존재하여 그 표면에만 전하가 존재하면 된다. (ex: 도체) 구체적으로 면전하는 표면 근처 전위의 미분값(=전기장)에 비례하는 형태로 결정된다. (식 (2.5) 참고)
라플라스 방정식의 해의 성질에 대한 중요한 논의가 2가지 있는데, 다음의 블로그에서 설명을 잘해놔 링크해둔다. 전자기학 10) 전위와 라플라스 방정식(Electric potential and Laplace Equation) : 네이버 블로그 (naver.com)
전자기학 10) 전위와 라플라스 방정식(Electric potential and Laplace Equation)
전자기학에서는 특히 전위(V, potential)에 대한 라플라스 방정식을 풀 일이 허다합니다. 그것은 주어진 ...
blog.naver.com
푸아송 방정식의 해는 이미 알고 있다. Phi(x)를 다음과 같이 이미 알고 있기 때문...

그래도 푸아송 방정식에 대입해서 확인해보는 과정은 필요하다. 그러나 라플라시안을 구해보면? singularity를 맞닥뜨린다.
이를 피하기 위해 퍼텐셜에 파라미터 a를 다음과 같이 추가하고, a를 0으로 극한으로 보내어 구해보도록 하자.

Phi_a(x)의 라플라시안을 계산하면 다음과 같다. 이때 r=x-x'로, 원점이 x'인 구면좌표계로 갔다고 생각하면 된다.

마지막에 등장한 f_a(r)이라는 함수는 a를 0으로 보낼 때 다음의 거동을 보인다.

즉 f_a(r)은 디랙-델타 함수였다!
(이는 사실 다음을 보이는 것과 동일한 과정이다.)

따라서 다음과 같이 마무리 지을 수 있다.

그러나 이런 디랙-델타 함수를 쓰지 않고 보이는 방법도 있다. 이게 잭슨에 나온 방법.

[ ] 괄호 앞에 곱해져있는 f_a(r)은 특정 길이 R 이상에선 사실상 값이 0에 가까우므로, 적분구간을 r=0에서 r=R까지로 제한하는 근사를 취할 수 있다.

따라서 다음과 같이 계산할 수 있다. d^3 x' = 4pi r^2 dr 을 대입하였기에 맨 앞 분모의 4pi가 사라졌다.

a->0으로 보내면 같은 결과를 얻을 수 있다.
1.8 Green's Theorem
지금까지 본 퍼텐셜 식은 푸아송 방정식의 해, 정확히는 경계조건(boundary condition)이 없을 때의 해이다. 경계조건이 간단한 특수한 경우에는 뒤에서 다룰 영상법(image of charge)을 이용하면 기존의 공식을 이용해서도 퍼텐셜을 구할 수 있으나(=전체 공간에서의 퍼텐셜의 값을 결정할 수 있다), 일반적인 경우에 대해선 새로운 방법이 필요하다. 그린함수(Green's function)를 이용한 방법이 바로 그것이다.
스칼라 함수(스칼라장) phi, psi에 대해 다음의 두 등식이 성립한다.
1) Green's first identity
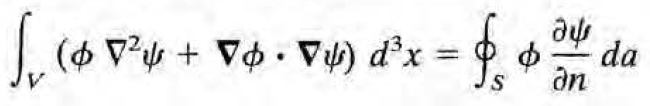
2) Green's second identity (or Green's theorem)
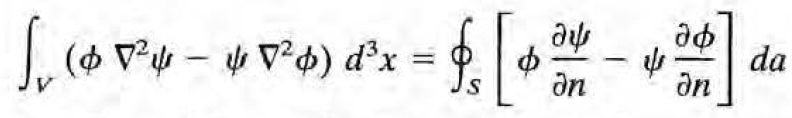
유도)
다음의 두가지 등식과 발산정리를 이용하여 쉽게 유도 가능.
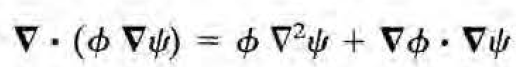
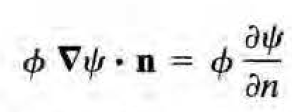
이제 Green's 2nd identity에 다음을 대입하자. 왜 굳이 저런 형태의 psi를 넣는지는 1.10절에 가서 나올 것이다.
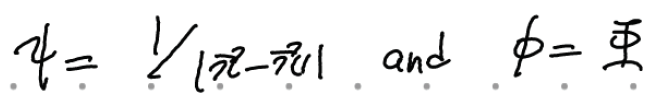

정리하면 다음과 같이 퍼텐셜을 구할 수 있다! 이것이 우리가 boundary condition이 존재할 때 항상 요긴하게 쓸 수 있는 general한 공식이다. (참고로 우변에도 Phi(x)가 있어 완전히 닫힌 꼴로 풀린 것은 아니다.) (사실 더 general한 식이 밑에서 green's function 얘기와 함께 등장한다)
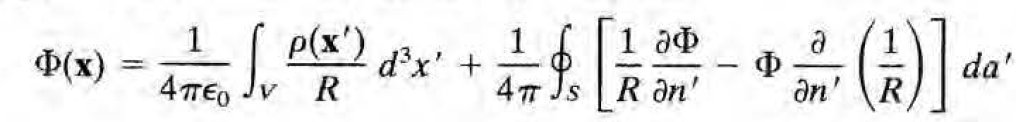
이때 점 x는 volume V 안의 점이다. 밖의 점을 고를 경우, 식의 값은 0이 된다.
수식) int_v Phi(x') delta(x-x') d^3 x' = 0 으로부터 우변이 0이 됨.
이유) 우변의 뒷항인 surface term의 두 항을 각각 다음과 같이 해석할 수 있다. (그리고 이 해석은 비단 지금의 논의에서뿐만 아니라 실제로 surface에 유도되는 면전하 등을 구하는데 있어서도 중요하다!)
괄호 안 첫 항: surface charge
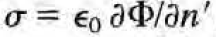
가 만드는 퍼텐셜
괄호 안 뒷 항:
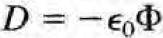
인 dipole layer가 만드는 퍼텐셜 (입체각을 이용하여 정리하기 전 식과 비교하여 볼것. n dot del'이 d/dn' 와 같음을 상기할 것)
면전하는 전기장의 discontinuity를, 쌍극자면은 퍼텐셜의 discontinuity를 만든다는 것을 기억하자.
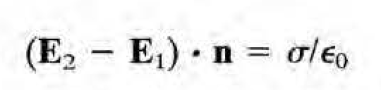
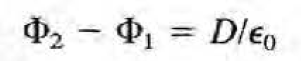
이제 보이고자 할 것은 "부피 V 안의 공간전하가 만드는 퍼텐셜(=첫 항)과 전기장이 표면 S를 넘어갈 때 discontinuity만큼 변화하게 되는데, 그 변화량이 정확히 공간전하가 만드는 퍼텐셜과 전기장을 상쇄하게 되고, 그로 인해 부피 V 밖의 전기장과 퍼텐셜은 둘다 0이 된다"는 것이다. 잭슨은 말로만 때웠는데 간단히 보일 수 있다.
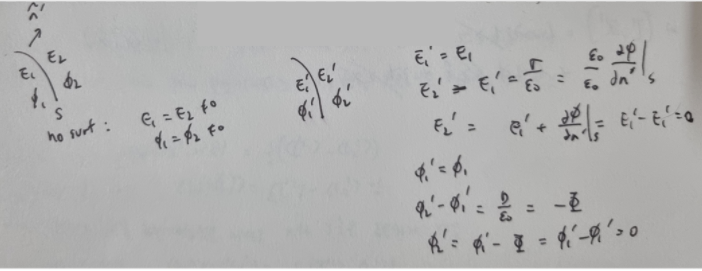
surface term이 없을 때, surface 직전의 퍼텐셜을 phi_1, 전기장의 normal 성분을 E1, surface 직후의 퍼텐셜을 phi_2, 전기장의 normal 성분을 E2라고 둔것. surface term을 넣고나서(즉 면전하와 쌍극자층을 넣고)의 것들은 prime을 붙였다.
E1'=E1, phi1' =phi1인것은 아직 surface에 닿지 않았기 때문이다.
저 중에 살짝 꺼려질 수 있는게 E2' 을 유도할 때 dphi/dn' at S 인데, 왜 surface 직전과 직후 중 직전의 퍼텐셜의 미분값을 쓴거냐 혹은 at S인데 왜 직전이나 직후의 값을 쓰느냐(이건 당연하게도 직전과 직후의 값이 다르기 때문에 정확히 S에서의 값은 정의되지 않기 때문) 같은 의구심이 들 수 있다. 저 d/dn' at S는 위의 Phi(x) 의 surface term 중 첫항을 면전하로 해석할 때 나온 것인데, 이 d/dn' 은 Green's 2nd identity에서 온거고, 이는 n dot del' 에서 온 것이다. 적분기호까지 같이 따라가며 생각해주면 결국 발산정리의 surface term을 어디서 계산하냐와 동일한 문제이고, 발산정리는 부피 내부의 요소가 표면 근처에서 어떤 영향을 주느냐를 말해주는 것이기 때문에 표면 바로 안쪽과 바깥쪽 중 어디서 계산하는 것이 옳으냐 하면 안쪽에서 계산하는 것이 표면의 영향을 받지 않을 수 있기 때문에 맞다.
위에서 퍼텐셜의 general한 식을 구했는데, 이에 대해 두가지 언급할 것이 있다.
1) S->inf 로 보낼 때: 퍼텐셜 Phi는 1/R보다 조금 더 빠르게 감소하기 때문에 surface term ->0 으로 간다. 즉 boundary condition이 없을 때의 퍼텐셜 공식이 다시 얻어짐.
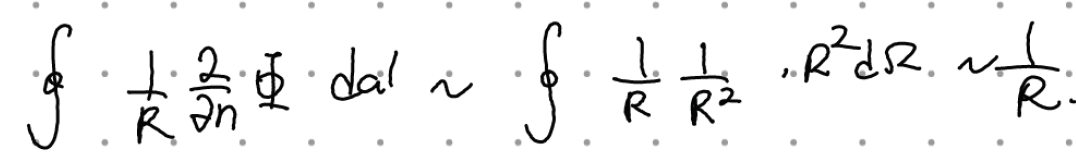
개인적으로 생각하는 함의: 위에서 닫힌 표면이 있고 그 안에만 공간전하가 분포하고 표면의 경계조건이 존재할 때 그 부피 밖의 퍼텐셜은 항상 0이라고 했는데, 점전하 하나 달랑 있고 경계조건이 없으면 무한한 거리에서도 퍼텐셜이 나온다. 이 두 상황을 경계조건의 유무로 구분짓고 아예 다른 상황이니 다른 결과가 나오는 것이라고 생각할수도 있겠지만, 후자의 상황을 경계가 무한한 거리에 존재하는 상황으로 이해해도 된다는 것이다.
2) rho=0일 때, 즉 라플라스 방정식의 해는 오로지 surface term에서만 온다. 즉 surface에서의 퍼텐셜에 관한 조건만 결정된다면 surface 내부 전체의 퍼텐셜이 전부 결정된다는 것이다. (외부는 0이므로 신경 안써도 됨)
1.9 Uniqueness of the Solution with Dirichlet or Neumann Boundary Conditions
해를 유일하게 결정하는 경계 조건의 종류와 그 이유에 대한 파트다.
수리물리 등지에서 편미방의 경계조건을 얘기할 땐 다음의 3가지 경계조건이 튀어나온다.
(1) 디리클레 경계조건 (Dirichlet bdry condi) : 경계면의 모든 위치에 대해 함수값을 지정
(2) 노이만 경계조건 (Neumann bdry condi) : 경계면의 모든 위치에 대해 함수의 미분값(normal derivative)을 지정
(3) 코시 경계조건 (Cauchy bdry condi) : (1)+(2)
우리가 지금 풀고 있는 라플라스, 푸아송 방정식에서는 (1), (2)가 쓰인다. (= (1) 또는 (2)가 주어지는 상황에 대해 해가 유일하게 결정되어 문제를 신명나게 풀수 있다) (3)은 overspecify, 즉 너무 많은 조건이다. 왜 하필 그러냐? 수리물리책을 펴면 나온다. 코시 조건은 closed boundary말고, open boundary일 때 많이 쓰이는 조건이다. 그럼 open bdry의 electrostatic 문제를 풀 때는 쓰일 수 있느냐? 결론은 electostatic problem은 closed bdry with (1) or (2)일 때만 결정될 수 있다고 한다.
보이는 방법은 쉽다.
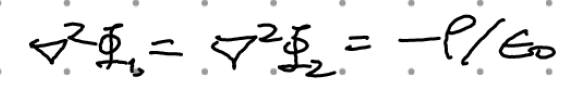
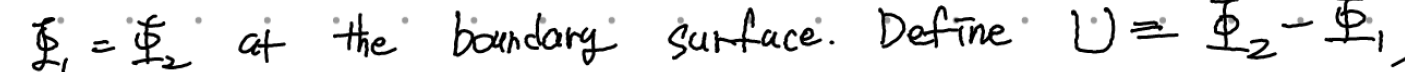
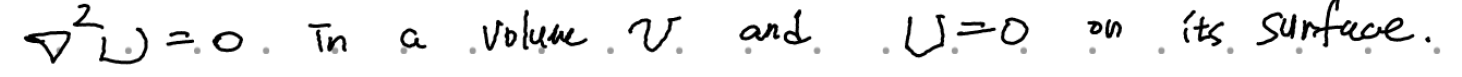
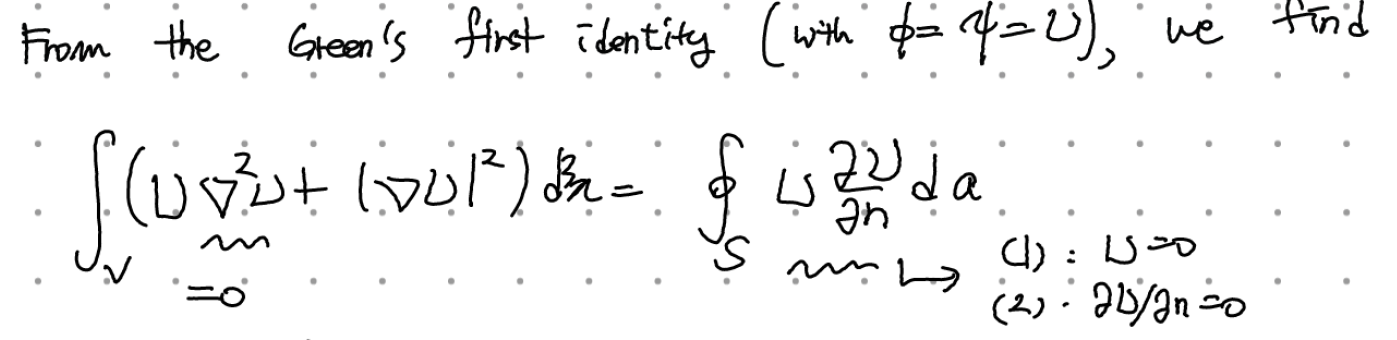
임의의 V에 대해 성립해야 하므로. 우연찮게도 U dU/dn이 모든 경계면에서 0이 되지만 (1)도 (2)도 아닐 수도 있는 상황이 있을수도 있는거 아니냐(어떤점에선 U=0 다른점에선 dU/dn=0 이런식으로 번갈아가며 0이 되기를 모든 점에서)라는 생각도 들지만 이런 조건은 현실적이지 못하다. 여튼 (1)이나 (2) 같은 조건을 주게 되면, 우변은 0인데 좌변의 | del U |^2 >=0이므로 공간 내 모든 곳에서 del U= 0이 된다. (1)이면 당연히 이게 되고, (2)이면 Phi 1 과 Phi2가 constant 만큼 차이날 수 있는 가능성이 여전히 존재하나, 전기장은 유일하게 결정될 수 있음이 보장되기에 상황이 유일하게 결정됨은 변하지 않는다(전기장은 단위전하당 힘으로 관측가능하며, 퍼텐셜은 관측가능하지 않기 때문에 관측가능한 물리량에 한해선 상황이 유일하게 결정됨 = 물리적인 상황이 유일하게 결정됨)
사실 디리클레 조건은 표면에서의 퍼텐셜을 결정하는 것과 같고, 노이만 조건은 표면에서의 수직 방향 전기장을 결정하는 것과 같다.
1.10 Formal Solution of Electrostatic Boundary-Value Problem with Green Function
위에서 왜 굳이 psi에 1/|x'-x|을 넣었는지에 대한 이유를 설명할 차례다. 푸아송 방정식의 미분연산자(=라플라시안)를 이 함수에 취했을 때 우변에서 디랙-델타 함수가 나오기 때문이다. (4pi는 notation마다 붙기도 하고 아니기도 하는데 잭슨은 4pi를 붙이는 notation을 취한다. 잭슨 문제 풀 때 유의.)
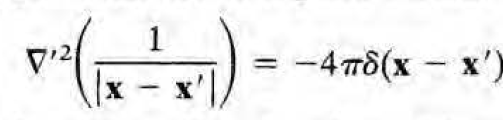
이는 공간전하밀도 rho가 디랙-델타(에 비례)일 때의 푸아송 방정식의 해로 볼 수도 있는데, 이는 점전하가 만드는 퍼텐셜이라는 것과 같고 실제 형태도 우리가 아는 것과 동일하다. 하지만 여기서 더 중요한 점은, 우리가 공간전하분포를 점전하->점전하 여러개(discrete)-> 공간전하분포(continuous)로 일반화해왔던 과정을 거쳐왔기에 이 함수를 통해 일반적인 전하분포가 만드는 퍼텐셜을 구할 수 있다는 것이다. (수리물리 시간에 Green's function을 배웠다면 다 아는 내용일것) 그래도 그 과정을 소개하면 다음과 같다.
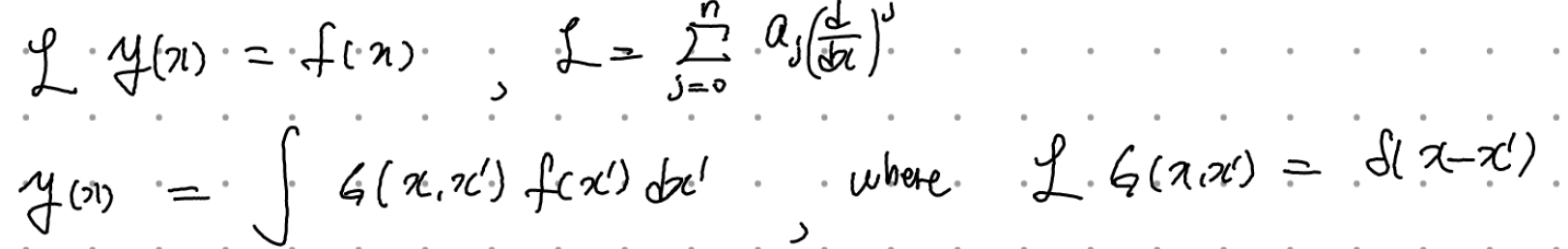
이제 (푸아송 방정식의) Green's function을 다음과 같은 방정식을 만족하는 함수 G(x,x')로 정의하자.
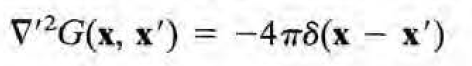
(G의 x<->x' 대칭성을 생각해보면
그럼 일반적인 G(x,x')은 다음과 같이 구해진다.
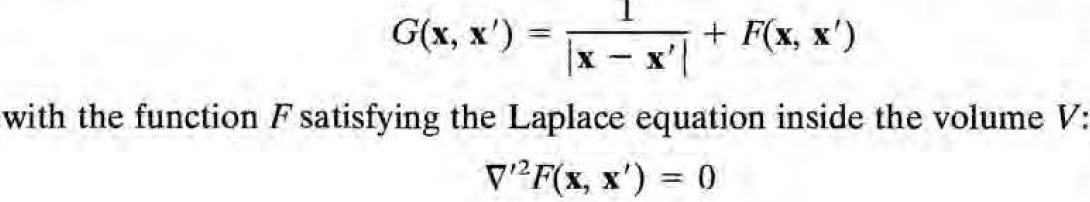
이제 위에서 구한 general한 퍼텐셜 식을 구할 때 Green's 2nd identity에 psi에 1/|x-x'| 대신 G(x,x')를 대입하여 구해보자.
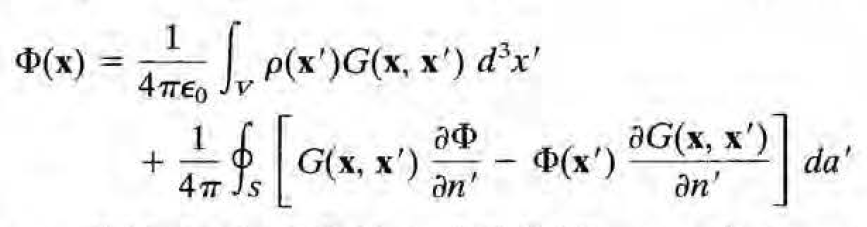
이제 G에 F라는 degree of freedom이 생겼으므로 boundary condition을 어떻게 잘 잡아주면 F의 자유도가 surface term의 두 항 중 하나를 날려버릴 수 있고, 퍼텐셜 식을 보다 간단하게 바꿀 수 있다. 그러한 boundary condition들이 사실 위에서 언급한 디리클레 조건과 노이만 조건이고, 각 조건에서의 Green's function G는 다음과 같다(=각 조건에서 F가 특정되고, 그 F 하에서 G가 다음과 같이 나타난다).

또 (2)에서 왜 굳이 dG_N/dn = -4pi/(surface area)여야 하는지 의문이 있을수 있다. 위에서도 약간 논의했지만, 우리가 지금 찾는 boundary condition들은 퍼텐셜을 유일하게 결정할수 있는 조건들을 찾는 것이다. 즉 충분조건을 찾는 것이다. 필요충분조건을 구하는 것이 아니다. 즉, 퍼텐셜을 유일하게 결정할 수 있는 '모든' 조건을 빠짐없이 찾고 있는게 아니라, 쉽고 실용적인 조건 몇가지만 구한다는 것이다. 그래서 (2)에서도 생각할 수 있는 가장 간단한 조건을 찾은거고, 우변을 -4pi/(surface area)로 둔 것이다.
(1) 조건 하에서 G는
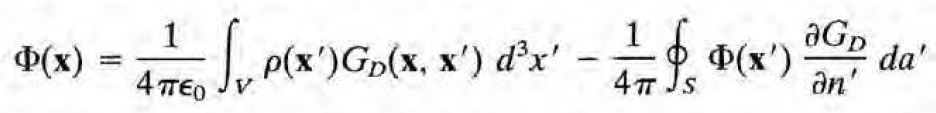
(2) 조건 하에서 G는
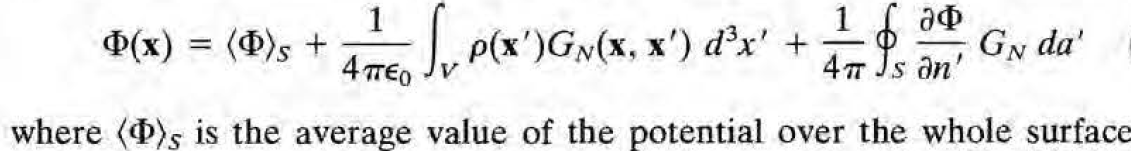
그린함수의 성질에 대해 몇가지 언급할게 있다.
(1) 그린함수 G는 구체적인 boundary value에 의존하지 않는다. 오로지 surface의 모양(geometry)에만 의존한다. 가령 디리클레 조건 하에선 표면에서 퍼텐셜 값이 특정되고, 그 값은 표면상 위치에 따라 임의의 값을 지닐 수 있다. 그러나 표면에서의 퍼텐셜 값이 뭐가 되었든 간에 표면에서의 G의 값은 항상 0이다. geometry 의존이란건 노이만 조건에서 surface area 때문에 들어간 말.
(2) G(x,x')=G(x',x)가 성립한다. G(x,x')에서 x는 observer, x'는 source charge의 위치로 해석해왔으므로, observer와 source charge의 위치를 바꿀수 있다는 물리적 의미가 있다.(개인적으로 이로부터 뭔가 유의미한 통찰을 얻어낼 수 있는게 있는지 모르겠다. 물리적 의미보다는 수식 정리 시 쓰임새가 있다고 생각 - 3장에서 중요하게 쓰일 때가 온다) 보이는 방법은 잭슨에서 설명.
(3) F(x,x')의 물리적 의미:
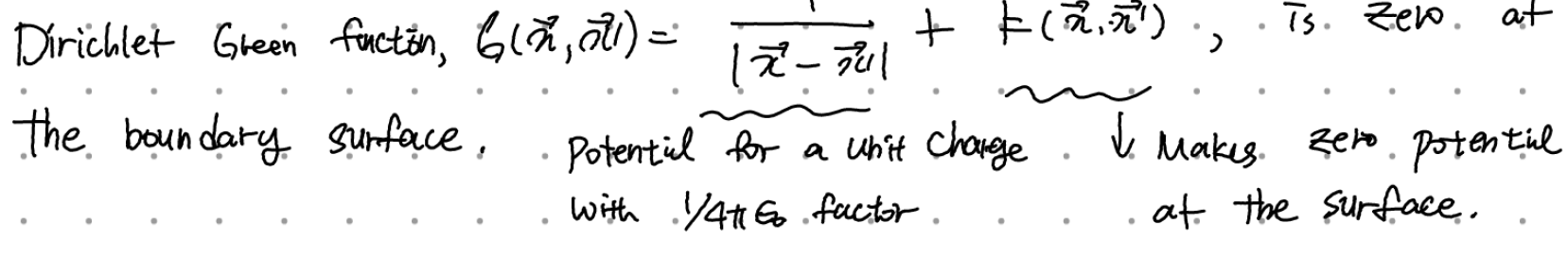

그리고, F(x, x')/4pieps0은 부피 내에서의 라플라스 방정식 (푸아송 방정식의 우변이 0) 의 해이기도 한데, 이는 부피 밖(=표면 밖)의 전하가 만드는 퍼텐셜으로도 볼 수 있다. 부피 밖의 전하는 부피 내의 퍼텐셜에 영향을 못 주기 때문이다. (표면에서의 경계조건이 주어지므로 외부의 효과는 차단되는 느낌)
위 두 사실을 종합했을 때, F(x,x')/4pi eps0 은 영상법(image of charge)에서 단위전하량을 가지는 가상전하가 만드는 퍼텐셜이라고 볼 수 있다!
가상전하를 둘 때 표면에서의 퍼텐셜이 0이 되도록 설정하던 것을 상기하라.
노이만 조건에서의 영상법: 이론상 dG/dn = -4pi/(area)가 만족되는 F를 찾을 수 있고 그 F에 해당하는 가상전하(분포)를 찾을 수 있다면 가능하겠으나, 디리클레 조건에서처럼 직관적으로 찾기란 거의 불가능할 것으로 보인다. 아마 문제에서 볼 일은 없을 것.
1.11 Electrostatic Potential Energy and Energy Density; Capacitance
학부 수준, 생략. 시간나면 추가
1.12, 1.13
너무 테크니컬. 생략.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
|---|---|
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |
| [잭슨 전자기학] Ch2 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (1/2): 전기장, 전위, 가우스법칙, 쌍극자층 (0) | 2024.09.29 |
| 잭슨 전자기학 정리 (0) | 2024.09.29 |