3.5 Associated Legendre Functions and the Spherical Harmonics
이제 원통대칭성이 없는 경우도 다뤄볼 차례다. 원통대칭성이 없으면 구속조건이 풀리며 m=0 외의 값도 허용되고, 따라서 associated Legendre polynomial이 등장하게 된다.
간략하게 몇가지 특징만 알아보면,




( 참고로 Condon-Shortley Phase라 불리는, (-1)^m factor는 잭슨에선 연관 르장드르 다항식의 정의에 포함시켰다. 만약 포함시키지 않는 정의를 택한다면 (-1)^m factor는 spherical harmonics에서 등장하게 된다. 보통 후자의 정의를 양자역학에서 주로 택하게 된다. [이유? 나중에 여유되면 추가})
위의 직교성으로부터, ortho'normal'한 basis를 적어주기 위해 규격화 상수를 곁들여 다음과 같이 구면조화함수(spherical harmonics)를 정의하자.

뒤에

다음은 몇가지 성질이다.
(1)

(2) orthonormal condition

(3) completeness relation

그외에 언급할 만한 내용으로는
(4)

(5) theta = 0일 때 nonvanishing Y_lm은 m=0인 경우 뿐이다. 즉
(6) 각종 점화식(recurrence relation)
(7) 양자역학과의 연관성 : 구체적인 설명은 생략.

(8) 참고할만한 자료
-아프켄 등 수리물리책
-잭슨
- Chapter 4: Spherical Harmonics | Physics (uoguelph.ca)
- Orthogonality of Associated Legendre Functions - ProofWiki
이제 구면조화함수를 이용해 다음과 같이 라플라스 방정식의 일반해를 구면좌표계에서 적을 수 있다. 어떤 대칭성이 존재하지 않아도 쓸 수 있는, 가장 일반적인 식이다.

3.6 Addition Theorem for Spherical Harmonics
제목을 잘보면 Additional theorem이 아니다! 추가적인 정리들을 다루는 게 아니라, <Addition Theorem>이라는 이름의 정리를 소개하려는 것이다.


이는 unit sphere 위에 존재하는 두 점 x (1, theta, phi) , x' (1, theta', phi) 에 대해 벡터 x, x'의 내적값을 인수로 받는 르장드르 다항식이 다음과 같이 두 구면조화함수의 곱의 합으로 전개될 수 있음을 말한다.
이를 이전에 3.3절에서 구했던 공식에 대입하면 다음과 같은 식도 얻을 수 있다.

이제 addition theorem을 증명할 차례인데.. 귀찮아! 넘길래! 소개는 안하겠지만 그래도 읽어볼 가치가 있는 증명이다.
3.7, 3.8 원통좌표계에서의 경계값문제
3.11절과 함께 뒤로 넘겨서 함께 다룰 것이다.
3.9 Expansion of Green Functions in Spherical Coordinates
이 작업을 하는 이유는 간단하다. 주어진 경계가 특정 좌표계에서 편하게 표현되면(eg 구 표면) 퍼텐셜도 그 좌표계에서 간단하게 표현될거고, 그린 함수도 그 좌표계에서 표현할 수 있으면 퍼텐셜을 구하기 편할 것이기 때문이다.
우선 경계가 없을 때의 그린함수는 1/|x-x'|이었으므로 구면좌표계에서 표현하면 위에서 보였듯 다음과 같다.

바로 다음으로 볼 예시는 경계가 구면(r=a)으로 주어지고, 그 밖을 관심 영역으로 두는 경우다. (exterior case)
이 경계조건 및 관심영역에서의 그린함수는 2장에서 구했었다.
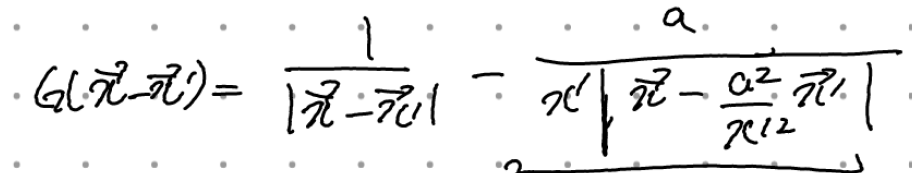
두번째 항을 정리할 차례다.
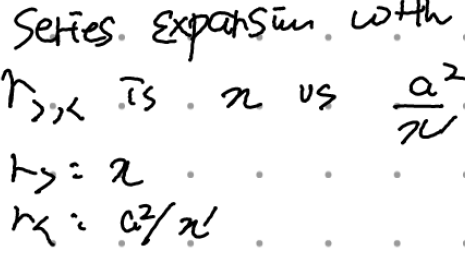
(r>와 r<가 왜 저렇게 되느냐: x는 observer point=구 밖, x>a, x'은 실제 점전하 위치 = 관심영역 안 = 구 밖, x'>a => a^2/x' < a
라플라스 방정식이든 푸아송방정식이든 그린함수는 (미분연산자에 의해 결정되기 때문에) 동일하고, 따라서 라플라스 방정식을 푸는 중이라 source charge가 없다고 한들 x'을 점전하의 위치라고 해석하는 건 문제없는 해석이다(푸아송으로 옮겼다 치면 되니).)
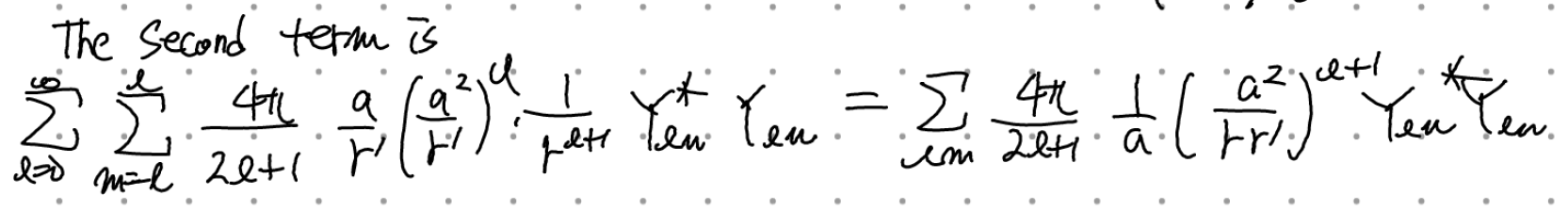
이제 두 항을 합쳐 정리하면

별표친 수식을 정리하면(r>, r<가 뭔지에 따라 정리)
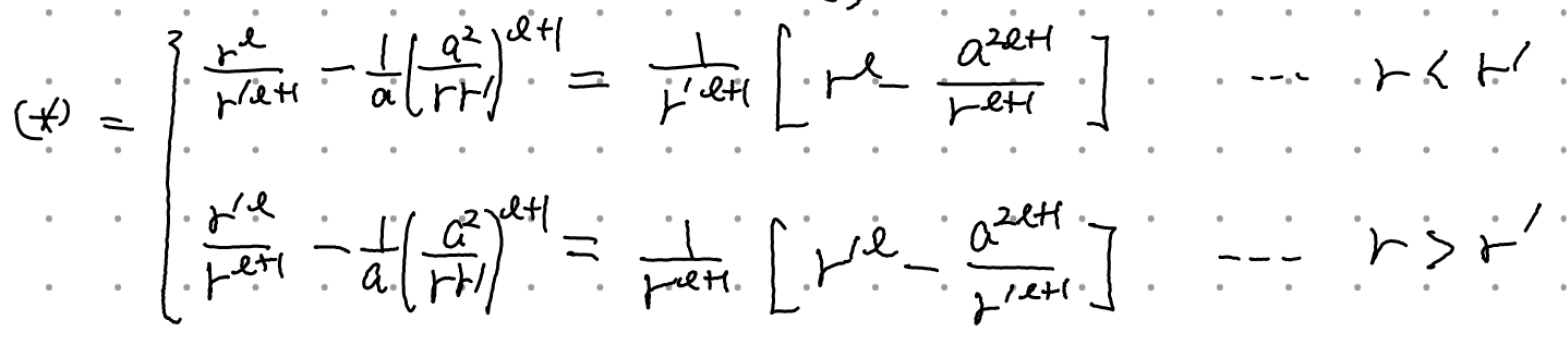
이 해의 특징에 대해 언급해야할 것들이 있다.
(1) r <-> r' 교환 성립 (그린함수의 성질 확인 가능)
(2) r=a (마찬가지로 r'=a)에서 G=0 : (디리클레 조건에서 그린함수=0이 됨을 확인 가능)
(3) r->inf (마찬가지로 r' ->inf)에서 radial factor -> 0
(4) r'을 고정시키고 r에 대한 함수로 보면, radial part는 r^l과 r^(-l-1)의 선형결합 : 라플라스 방정식의 해에서 봤던거와 동일. 이는 그린함수 자체가 source term이 디랙델타 함수인 푸아송 방정식의 해이기 때문.
여기까지 구한 건 구면 밖 관심영역에서의 그린 함수였다. 이제 보다 일반적인 경우의 그린함수를 구해보자.

우변 정리)
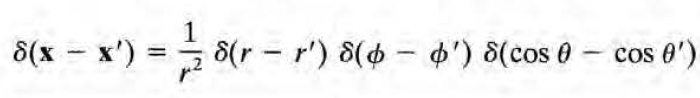
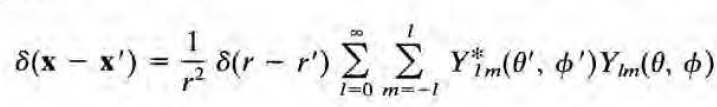
왜 3d 디랙델타가 구면좌표계로 갈때 1/r^2이라는 factor가 붙느냐:
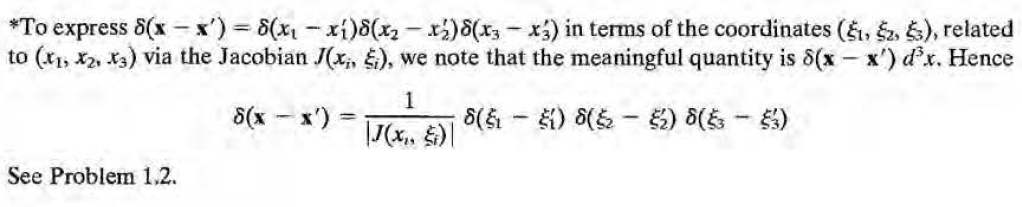
좌변 정리) G(x,x')을 x'을 고정하고 x에 대한 함수라고 여기고 미정계수 Alm을 도입하여 구면조화함수 기저에서 표현하면 다음과 같다.
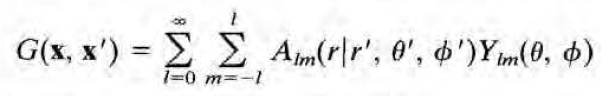
이제 이 둘을 위 미분방정식에 대입하여 정리하자.
그럼 Alm을 우측 미분방정식을 만족하는 g_l(r,r')을 이용하여 좌측 식으로 표현할 수 있다.
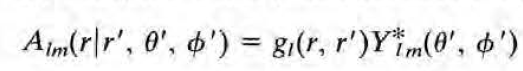
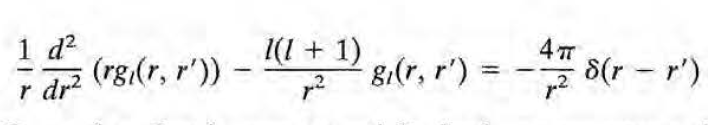
r != r' 일 경우 우측 미방은 homogenous DE가 되고, 풀면 다음과 같다.
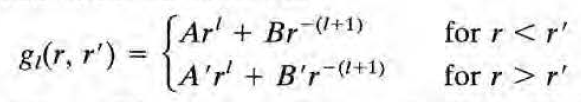
A,B,A',B'이라는 계수는 r'의 함수로, (1) 경계조건 (2) r=r'에서의 조건: 디랙델타 - dg/dr의 discontinuity (3) r <-> r' 대칭 이 3가지 조건을 적용함으로써 결정될 수 있다.
교재의 예시는 두 구 표면 r=a, r=b가 경계이고 그 사이가 관심영역인 경우이다. 구체적인 풀이는 안하고 논리 흐름만 소개하면
(1) 경계조건을 위의 g_l 식에 대입
(2) r<->r' 대칭을 이용하여 두 케이스로 나뉘어있던 g_l을 하나의 식으로 통합 (이 과정에서 r>, r<가 등장하고, 두 케이스의 곱의 상수배로 간단히 표현 가능)
(3) 마지막 남은 g_l의 overall constant factor를 r=r'에서의 조건 - dg/dr의 discontinuity를 이용해 결정
결과는 다음과 같다. 복잡해보이는데 유도과정을 읽어보고나서 보면 뭐가 뭐에 해당하는지 명확히 보여서 간단해보인다.
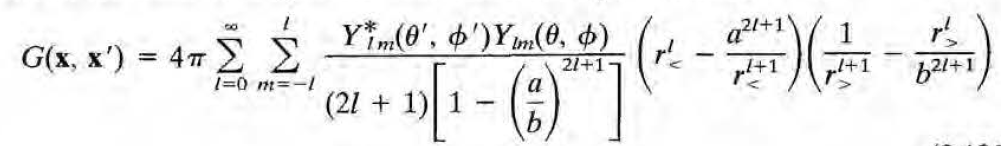
교재의 예시의 special case를 몇가지 얘기하자면,
a->0, b->inf : 경계가 없을 때의 G(= 1/|x-x'|) 로 감
a->0, b -> finite : 구 내부가 관심영역일 때의 G로 감
a-> finite, b-> inf: 구 외부가 관심영역일 때의 G로 감
직관적으로 예상되는 바가 나온다.
3.10 Solution of Potential Problems with the Spherical Green Function Expansion
이제 이렇게 구한 그린함수를 실제로 퍼텐셜을 구하는데 적용해보자.
디리클레 조건 하에서 퍼텐셜은 다음과 같았다.
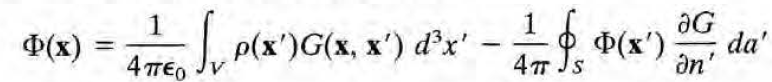
rho는 문제에서 주고, G는 구했고, Phi(x) at surface도 문제에서 경계조건으로 주니 우리가 더 알아야할 것은 dG/dn' 뿐이다.
n'의 방향은 관심영역 안에서 밖으로의 normal 방향. 예시로 interior case에 대해 구해보자.
이때의 그린함수는 (a=0, b is finite)
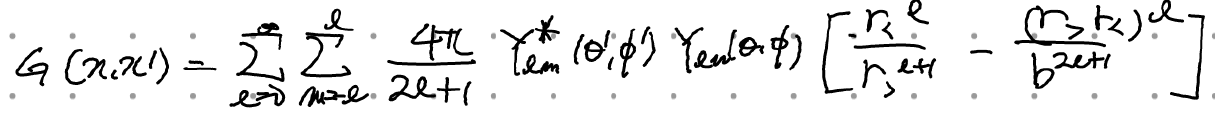
n'은 구 안에서 밖으로 나가는 방향이므로 r' 방향과 동일, 따라서 그린함수의 미분은
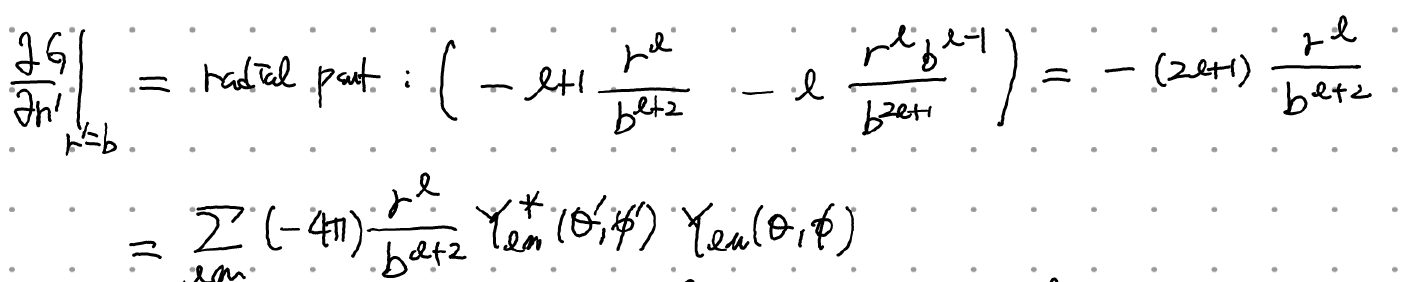
rho는 0이라 가정(=라플라스 방정식)하고, 구 표면에서의 전위를 V(theta', phi')라 하면 (r=b로 고정되므로 V는 r에 의존하지 않고 theta와 phi에만 의존) 퍼텐셜은 다음과 같다.
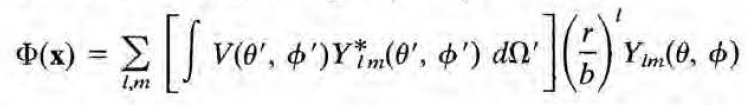
이는 2장에서 구했던 다음의 식의 interior version ( 분자가 a(a^2-x^2) )과 동일하다.
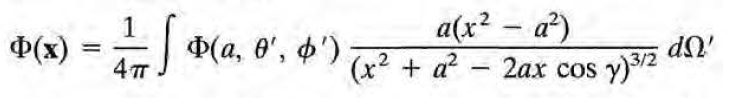
또 다른 예시 상황을 보자.
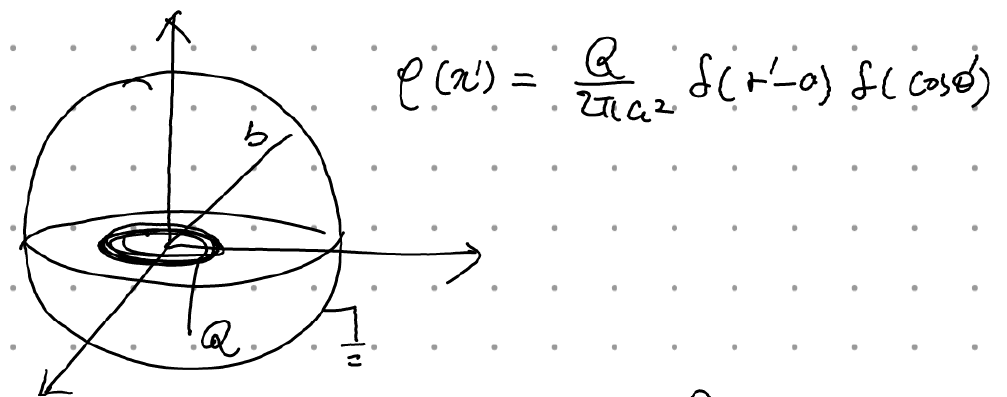
conducting, grounded, 반지름이 b인 구가 있고 그 안에 반지름이 a인 대전된 ring이 존재하는 상황.
우선 구 표면의 퍼텐셜이 0이므로 surface term은 0이다.
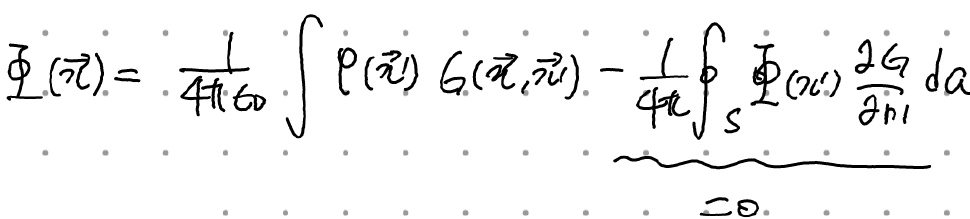
앞의 volume term만 계산하면 다음과 같다.
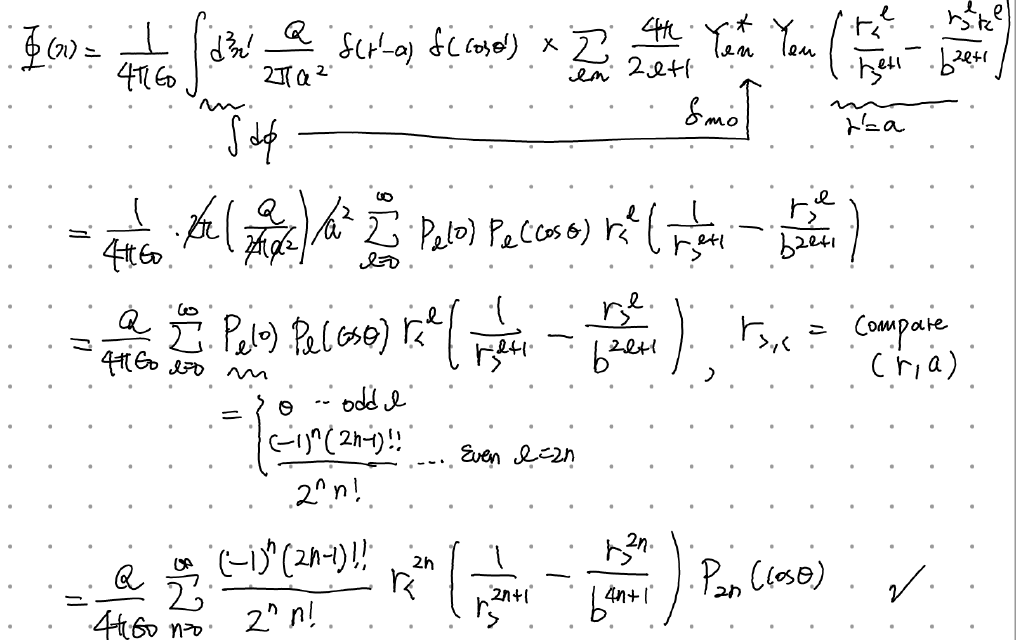
첫 줄을 해설하자면
int d^3 x' = int r'^2 dr' int sin theta' dtheta' int dphi' 인데, radial integral은 뒤의 delta(r'-a)와 만나 r'를 a로 치환하고 사라진다. 둘째줄에 나오는 a^2도 여기서 나온다. solid angle integral 파트는 다음 사진을 참고.
(맨 윗줄에 식 적을 때 d(cos theta')을 빼먹었어서 마지막에 황급히 추가. 그리고 사소한 오류가 있는데 sin theta' dtheta'는 d(cos theta')가 아니라 -d(cos theta')다. 전체 적분 구간이 -1 to 1이라 마이너스 부호를 적분 구간에 흡수시켜주면 되니 문제는 없음)
아무튼 이렇게 구 안의 링이 만드는 퍼텐셜을 구해봤고, b->inf로 보내면 우리가 아는 링이 만드는 퍼텐셜이 다시 recover된다.
교재에서는 한가지 예시를 더 소개한다. 이번엔 구 안의 선전하이다.
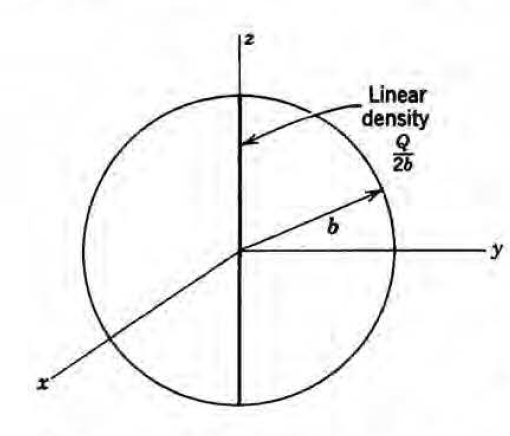
전하밀도는 다음과 같다.
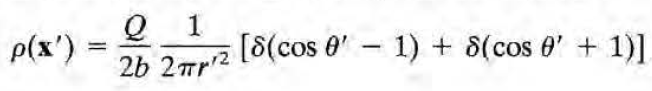
구하기 좀 어려울 수 있는데, 주어진 선전하는 theta=0(즉 z>0인 부분에 해당)일 때랑 theta=pi(즉 z<0인 부분에 해당)일 때의 두 구간으로 나눌 수 있다. 이 둘이 두 델타함수에 해당한다. 디랙델타 정리 테크닉에 대해서는 이 링크( mp03 (bilkent.edu.tr) ) 나 이 포스팅( 후추) 참조. 대략 설명하면 1/r'^2은 delta^(3)(x)의 구면좌표계 표현에서, 1/2pi는 원통대칭성에서 나온다.
퍼텐셜을 구하면 다음과 같다. 정리 시 사용되는 테크닉은 위의 ring 예시에서와 완벽히 동일.
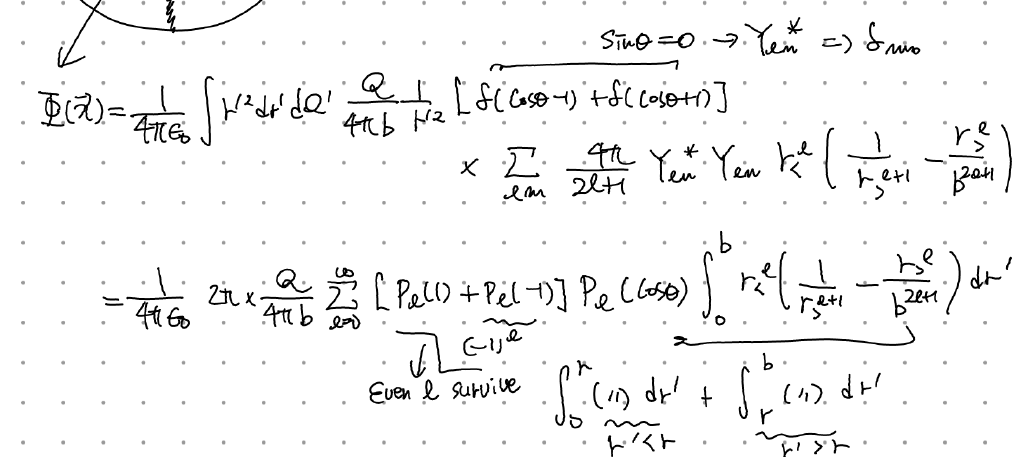
(오타:
이제 적분 파트만 계산하면 되고, 그 결과는 다음과 같다.
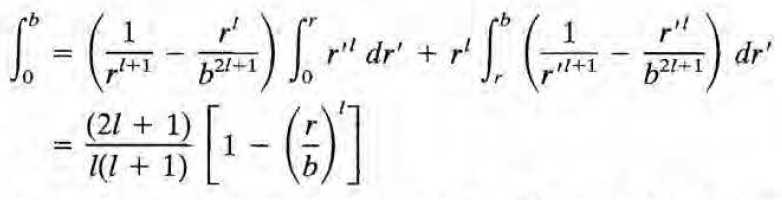
l=0일때의 값이 정의가 되지 않으므로, 로피탈의 정리를 이용해 구한다. (2l+1)/(l+1)은 l=0일 때 1임을 상기.
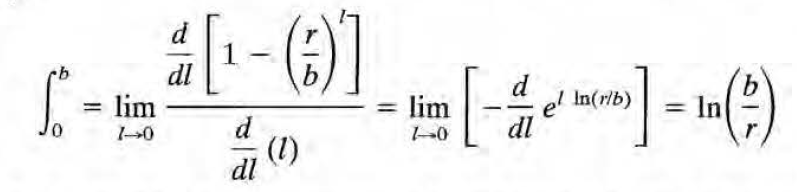
정리하면 다음과 같다.

log(b/r)은 경계가 없을 때 선전하가 만드는 퍼텐셜과 동일하다! 따라서 non-zero l에서 나오는 퍼텐셜은 전부 경계조건에 의해 만들어진 것(=구면에 유도된 면전하가 만드는 퍼텐셜)이다.
최종 결과를 정리하면 다음과 같다. 구면에 대전되는 면전하도 계산해보았다.
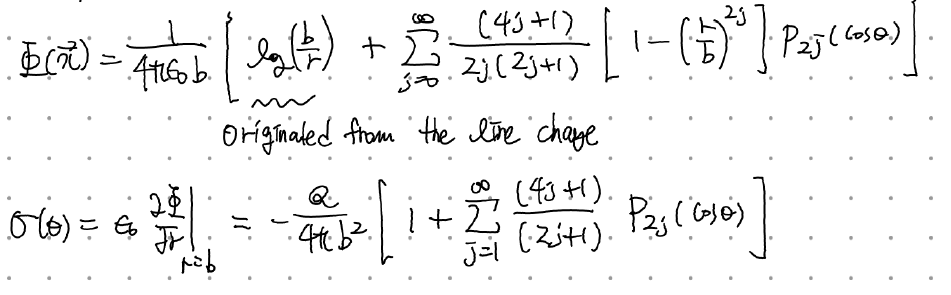
======
위키백과에 이런 문서가 있다. Spherical multipole moments - Wikipedia
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch3 - (4/4) (0) | 2024.10.05 |
|---|---|
| [잭슨 전자기학] Ch3 - (3/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |
| [잭슨 전자기학] Ch2 (0) | 2024.09.30 |
| [잭슨 전자기학] Ch1 - (2/2): 푸아송 방정식, 라플라스 방정식, 그린함수, 경계조건 (0) | 2024.09.30 |