(작성일: 2024-12-04 18:38)
7.10 Causality in the Connection Between D and E; Kramers-Kronig Relations
A. Nonlocality in Time
우리는 유전율 \(\epsilon\)이 frequency dependence를 가진다는 것으로부터 D와 E가 temporally nonlocal(=time difference)하다는 것을 알게 될 것이다. 다시 말해, 시간 t에서의 D가 시간 t에서의 E에만 의존하지 않는다는 것이다. 뒤에서 수식으로 유도하겠지만, 미리 스포하자면 시간 t에서의 D는 시간 t 이전의 모든 E에 의존하게 된다.
$$ \vec{D}(\vec{x},t) = \epsilon(\omega) \vec{E}(\vec{x}, \omega) $$
로부터 시작하자.
우리가 원하는 것은 위치 x와 시간 t에서의 E,D이니, 푸리에 변환을 하며 시작하자.


2->3줄: eps0을 뽑아냄
3줄: 첫항은 t'-t=tau로 치환한 것뿐. 뒷항은 이제 w 의존성이 exp 항 빼곤 없기 때문에 디락델타 뽑아내 정리한것.
4, 5, 6줄: 첫항에 대한 식. 이번엔 eps에 w의존성이 있어서 디락델타를 뽑아내진 못하고 대신 G(tau)라는 식 정의. 그리고 이 식을 들여다보면 eps/eps0 - 1의 푸리에 변환인데 이건 electric susceptibility \(\chi_e)라는걸 상기.
결론:

즉 다음과 같은 논의 가능. D(x,t)는 동일한 시간에서의 전기장 E(x,t)에도 의존하나, 다른 시간(t-tau, 그리고 tau를 모든 시간에 대해 적분하니 사실상 모든 시간)에서의 전기장에도 의존한다.

B. Simple Model for G(tau), Limitations
이제 구체적인 사례를 생각해보자. 앞전에 얘기했던 damped harmonic oscillator model을 가져와 논의하자. 먼저 G(tau), 즉 \(\chi_e(\omega)\)의 푸리에변환을 계산하자.

이 적분은 칸투어 적분을 통해 계산 가능하다. 다음과 같이 pole의 위치를 확인하고 기호를 정의하자.

경로를 다음과 같이 설정하자.

둘째줄의 첫항이 우리가 원하는 식 G(tau)이고, 뒷항은 R을 무한대로 보낼때 0으로 가므로, 결국 우리가 구하는 G(tau)는 세번째 식과 같이 구해진다(모르는 사람은 유수정리 참고).

우리의 식에선 다행히 residue가 쉽게 구해지는 편. 분모에서 0되는 항 빼고 w에 w1,2 대입하여 각 pole에 대한 residue가 구해진다. 마지막 줄에선 w1,2의 정의를 대입해서 계산을 마무리한것.
근데 이건 tau>0일 때의 얘기이다. tau>0일 때 뒷항이 R->inf에서 0으로 가려면 아래쪽 반원을 택해 적분해야하기 때문. 아래쪽 반원을 택할 경우 pole이 닫힌경로 안에 포함되게 되고 0이 아닌 값이 나올 수 있었던 거였다. tau<0일 때는 다음과 같이 위쪽 반원을 택해 계산해야하고, pole이 경로 안에 없기에 당연히 0이 나오게 된다.

둘을 합쳐 쓰면 다음과 같다. theta는 step function.

그래프를 그려보면 다음과 같다.

이제 이를 처음에 구한 식과 엮어서 논의해보자.

즉 D(x,t)가 t 외에 다른 시간의 전기장에도 의존한다 했지만, t보다 더 미래의 시간의 전기장의 의존성은 G=0과 곱해져 사라지게 된다. 즉 G가 tau의 부호에 따라 완전히 다른 결과가 나온 것은 인과성과 연관이 있었던 것.
정리하자면,


tau>0일 때 G의 개형도 얘기를 해보면, D(x,t)가 과거의 전기장에도 영향을 받는데 더 먼 과거의 전기장일 수록 그 의존성이 exponential하게 줄어든다는 것이고(동시에 진동도 하긴 한다만) 그 time scale은 \(1/\gamma\)로 주어진다는 것이다.
C. Causality and Analyticity Domain of \(\epsilon (\omega) \)

이 식은 uniform isotropic medium에서의 D와 E의 spatially linear, isotropic, causal한 관계를 보여주는 식이다.
다음의 식을 좀 더 살펴보자.

특징 (1)

특징 (2)

오타가 있는데 적분변수가 tau가 아니라 omega여야하고, exp항의 지수에 전부 (-)가 붙어야 한다. 첫 적분 식은 위쪽 반원에 대한 선적분을 말함. 우변의 첫항은 2pi*G(tau)와 같으므로 tau<0일 땐 첫항의 값이 0이 나오고, R->inf에서 두번째 항의 값 또한 0이 나온다. 따라서 좌변 또한 0이고, 이는 upper half plane 안에 pole이 존재하지 않음을 의미한다. 즉 eps/eps0 - 1은 upper half plane에서 항상 analytic하다는 것이다.
참고)
$$ G(\tau) = \frac{1}{2\pi} \int_{-\infty}^{\infty} d\omega (\frac{\epsilon(\omega)}{\epsilon_0}-1) e^{-i\omega \tau} $$
$$ \frac{\epsilon(\omega)}{\epsilon_0}-1 = \int_{-\infty}^{\infty} d\tau G(\tau) e^{i\omega \tau} = \int_{0}^{\infty} d\tau G(\tau) e^{i\omega \tau} ( \because G(\tau) =0 \ \text{at}\ \tau<0)$$
따라서 다음과 같이 정리할 수 있다. G(tau)가 실수임을 상기하자.

둘째 줄 첫항에서 w=inf 일 때 값이 0이 되어 셋째줄에서 안보이게 되었는데, 왜 0이 되냐 하면 upper half plane에서는 Im(w)>0, 즉 exp(iwt) = exp(-Im(w)t + iRe(w)t)에서 t->inf이면 절댓값이 0으로 가게 되기 때문이다.
마지막 줄에서 첫항이 0이 되는 이유는 G(0+)=G(0-)=0이기 때문. G가 불연속이라는 것은 물리적이지 않다.
.. high frequency => tau~0 조건은 어디서 쓰였는지 잘 모르겠다.
잠시 얘기할만한 사소한 디테일.

바로 윗윗 사진의 첫줄 수식이 (7.112)이다. 즉 첫문장은 우리가 위에서 유도했던 바로 그것을 말한다. 다음 문장은 현재 시간에서 tau->inf만큼 과거의 전기장의 영향(G)이 0으로 간다는, 물리적으로 합리적인 조건이 x축(=Re{w}축)에서의 eps(w)/eps0의 analyticity를 보장하는데 있어서 필요하다는 것을 말한다. 우리가 위에서 유도할 때 x축에서의 논의를 뭉갰던 셈이다. 그리고 이 물리적으로 합리적인것처럼 보이는 조건은 도체에서는 깨지게 되고, 그로 인해 x축에 pole이 하나 생기게 된다. 그 위치는 w=0, 즉 원점이다.

마지막으로 알아주면 좋은 susceptibility(동등하게, 유전상수, 혹은 굴절률)의 w-의존성이다. 실수부와 허수부의 의존성이 다른 것을 볼 수 있다.
D. Kramers-Kronig relation( Kramers–Kronig relations - Wikipedia)
결론부터 말하자면, Kramers-Kronig relation은 다음과 같은 관계식을 말하는 것으로 eps/eps0의 실수부와 허수부의 관계이다.
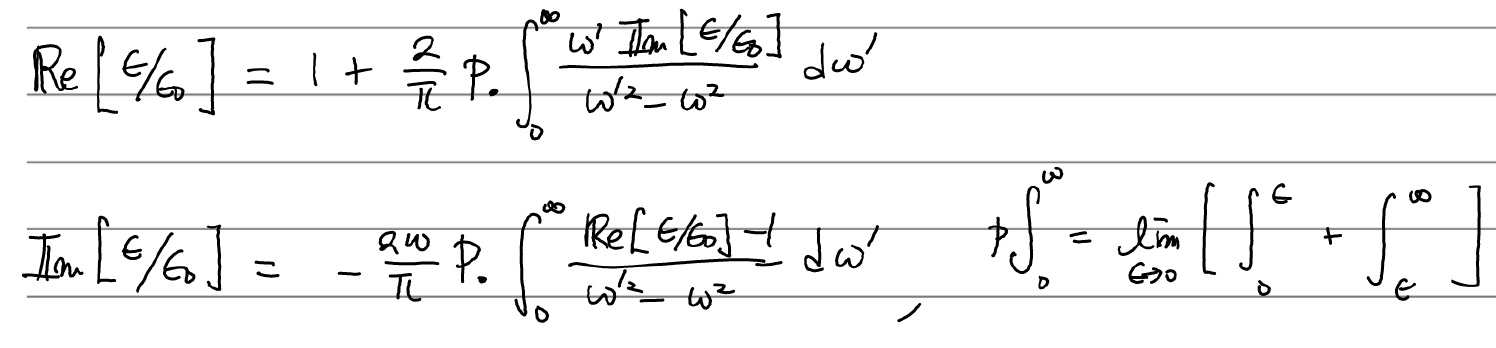
P는 Cauchy principal value( Cauchy principal value - Wikipedia)를 말하는 것으로, 실수 구간에서 적분 중에 발산하는 점 하나가 있으면 이를 빼고 적분하는 것을 말한다.
이제 이를 유도해보자.

eps(w)가 아니라 eps(z)가 됨에 유의. z는 upper half plane 위의 임의의 모든 복소수이다. 첫 줄의 식이 어디서 나왔냐 하면, 적분 안의 식처럼 분모에 w'-z를 넣어 z에 일부러 pole을 하나 만들어두고 유수정리를 써서 유도한것. upper half plane에서 eps는 원래 analytic하므로 닫힌경로 안에 존재하는 pole은 우리가 z에 일부러 만든 pole 하나밖에 존재하지 않게 된다.
둘째줄로부터 C에 대한 선적분이 곧 실수 구간(-inf~inf)에서의 적분으로 바뀌게 된다.
따라서 다음을 얻는다.

이제 다음의 극한을 생각하자.
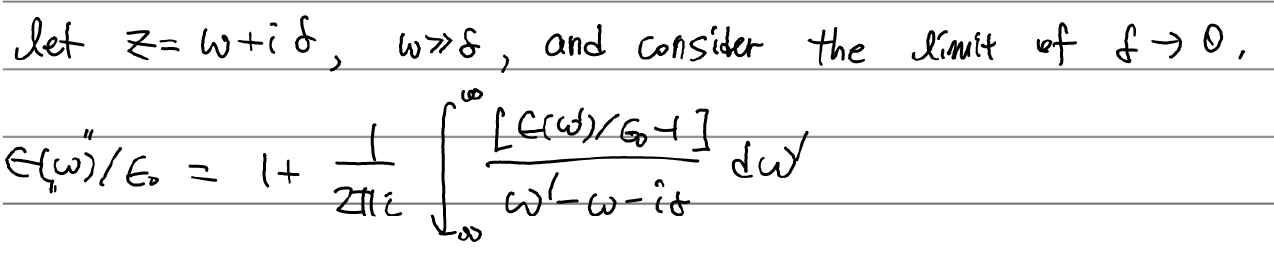
이제 다음의 공식을 하나 사용하자. 유도는 w+id에 pole을 가지고 있을 때 위쪽 반원으로 선적분해주는 과정에서 나온다. complex analysis - Proof of the Kramers-Kronig relation for amplitude and phase - Mathematics Stack Exchange 대충 여기 나오는 그림과 같은 느낌.

이를 대입하고 계산해주면 다음을 얻음. 뒷항은 적분과 디락델타가 만나서 정리된것.
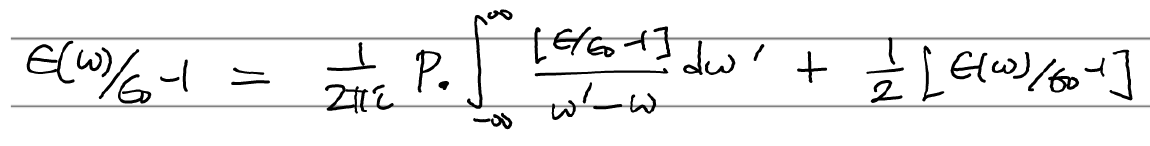

둘째줄은 위 식의 우변의 둘째항을 좌변으로 넘기고 양변 2배해주고 1더해 정리한 것.
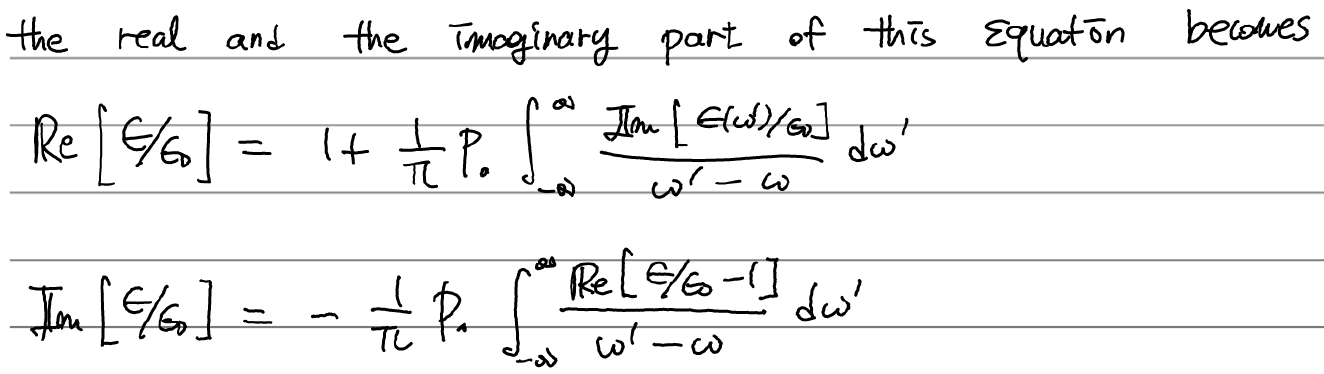
실수부와 허수부를 분리하였다. 참고로 위의 두 식은 이렇게 쓸 수도 있다.
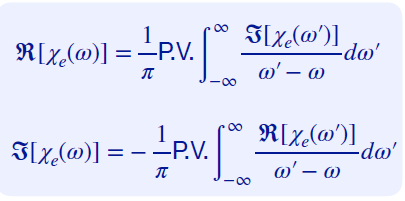
잠깐 아까 유도했던 특징 (1)로부터 다음을 얻자.
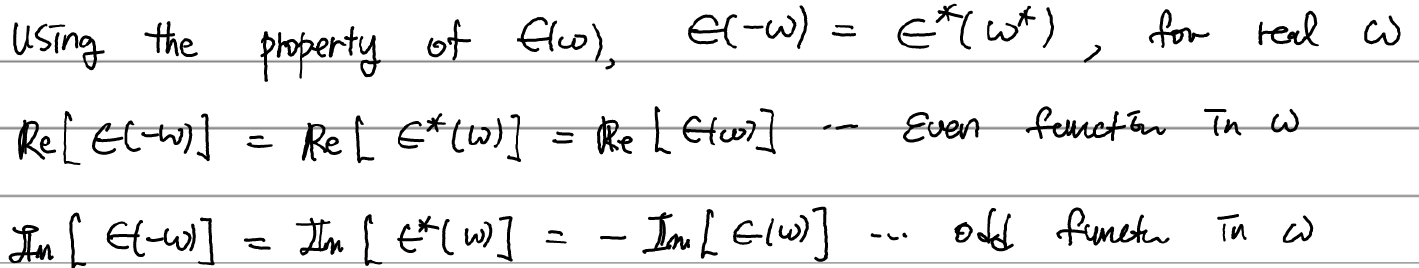
이제 이를 이용해 위의 적분을 정리해보자.
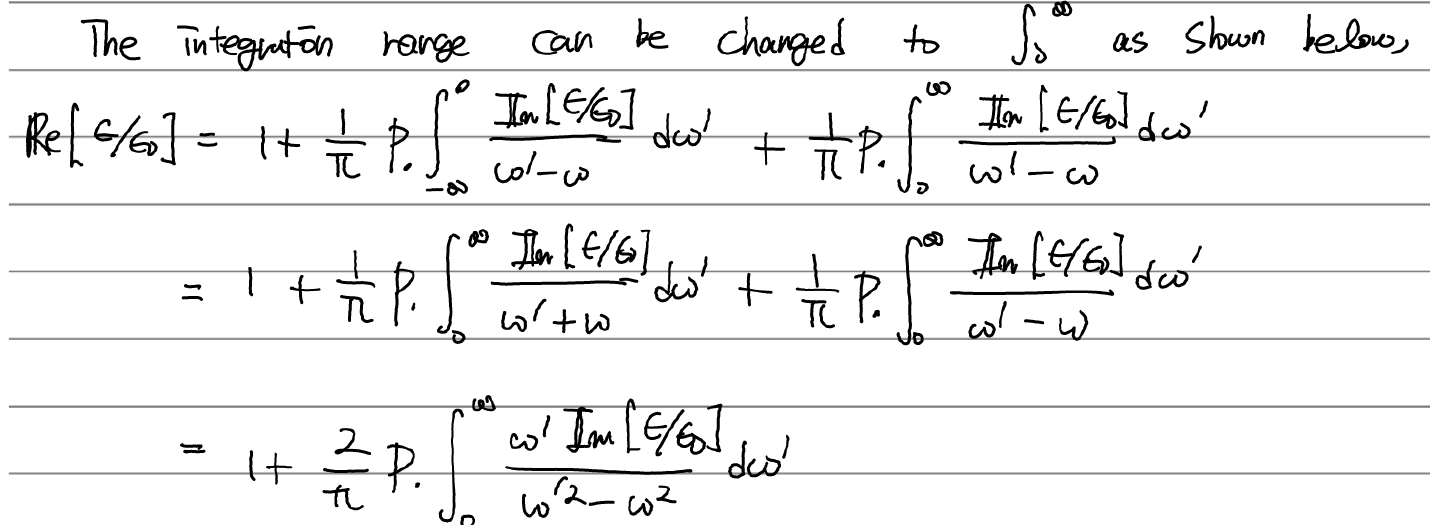
첫줄에서 둘째줄로 갈때 둘째항에서 w->-w로 바꿔주었다. 분자 Im(eps/eps0) 뿐만 아니라 분모도 odd funtion이니 전체식은 even function이 되어 변하지 않고, 적분 구간만 바뀌였다.
같은 방식으로 허수부에 대해서도 해주면
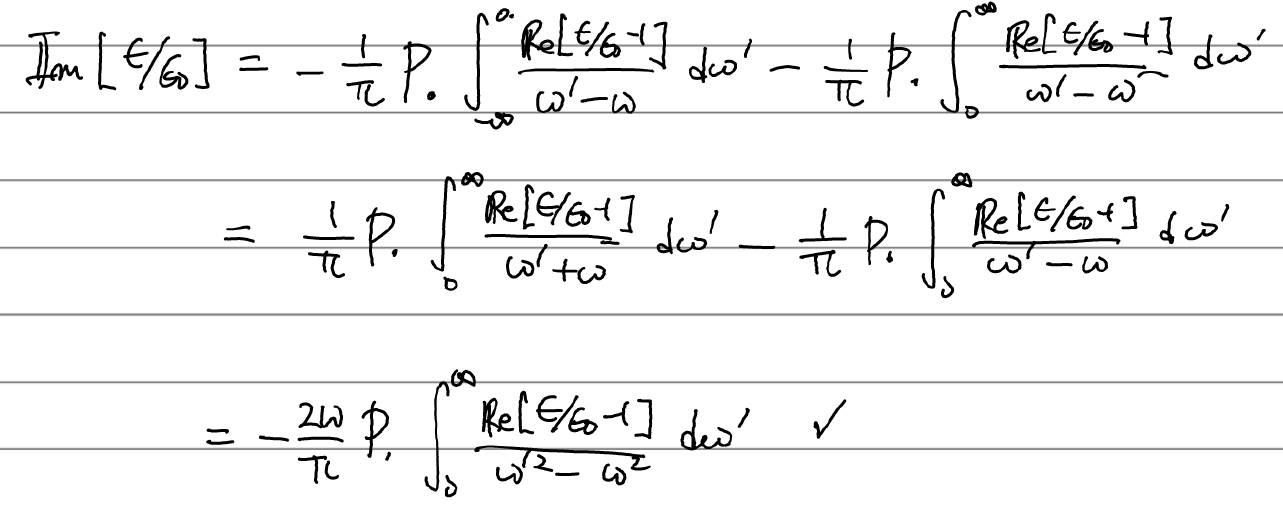
이렇게 유도가 끝이 났다. Re(eps/eps0)은 굴절률(=Re(eps(omega))과 상관이 있고, Im(eps/eps0)은 absorption coefficient(=Im(eps))와 상관이 있으니 이 관계식은 곧 굴절률과 흡수계수의 관계식으로 볼 수 있다.
이제 예시와 논의를 할 차례다.
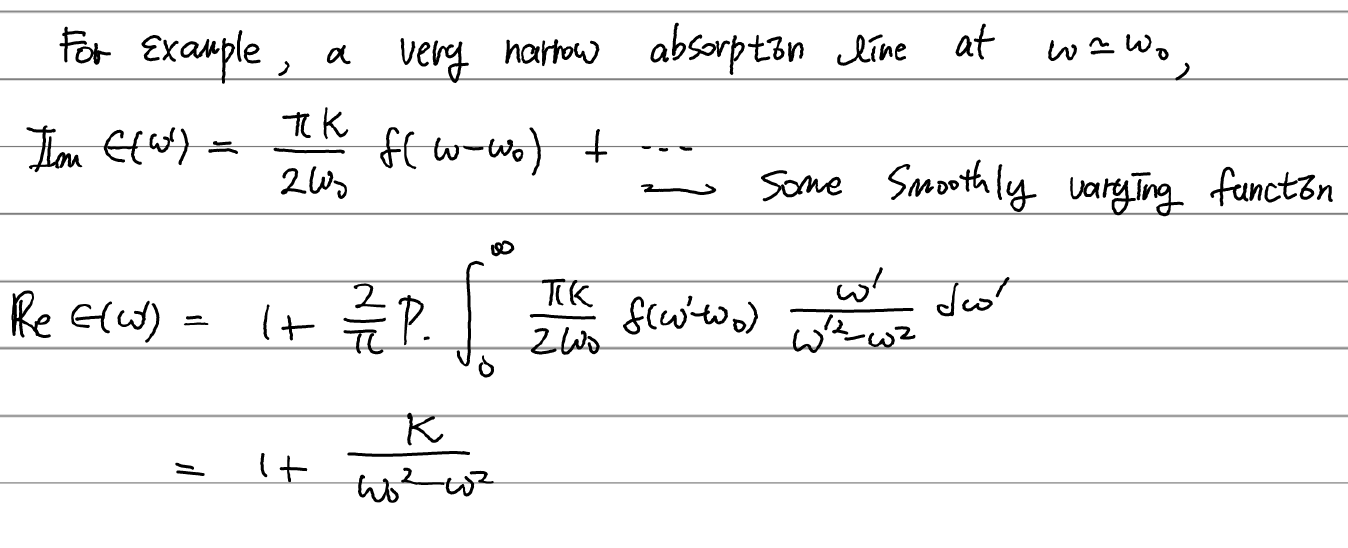
이 간단한 예시 외에도 우리가 계속 가지고 놀았던 damped harmonic oscillator model에 대해서도 구할 수 있는데, 직접 해보길 바란다. 연습문제에도 있는데, 계산량이 살벌하다..
마지막으로 두가지 sum rule을 소개한다. sum rule이 무슨 뜻으로 말한건진 잘 모르겠는데 아마 적분이 들어간 식이라서 그런거 아닐까 짐작만.

앞의 C절에서 얘기했던 것. 첫 식은 앞에서 구했던 다음의 두 식을 연립하여 얻어진다.
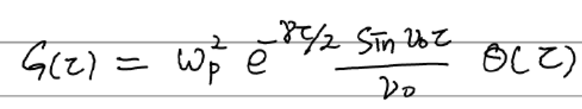
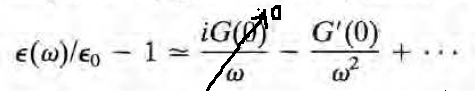

imaginary part는 w^-3으로 떨어지기에(C절의 마지막에서 구함) 식에 대입해봤자 w^-1이 되어 w->inf로 가면 영향이 사라지기에 real part만 넣어 계산하였다. 대충 하려면 분모의 w^2이 매우 크니 w^2 취급하여 앞의 w^2과 약분해주면 바로 나오고, 체계적으로 근사하려면 밖의 w^2을 적분식 안으로 넣어주고, 분모 분자 w^2으로 나눠주고, 분모의 식을 전개해주고(1/(1-x)=1+x+x^2+..) 첫항만 남기면 나온다. 이렇게 얻어진 식이 첫번째 sum rule.
두번째 sum rule은 다음과 같다.

N은 w보다 작은 어떤 실수. 마지막 식이 우리의 두번째 sum rule이다. N->inf로 보낼때의 논의가 있긴 하다만 그리 중요한지는 모르겠다.
유도과정은 다음과 같다.
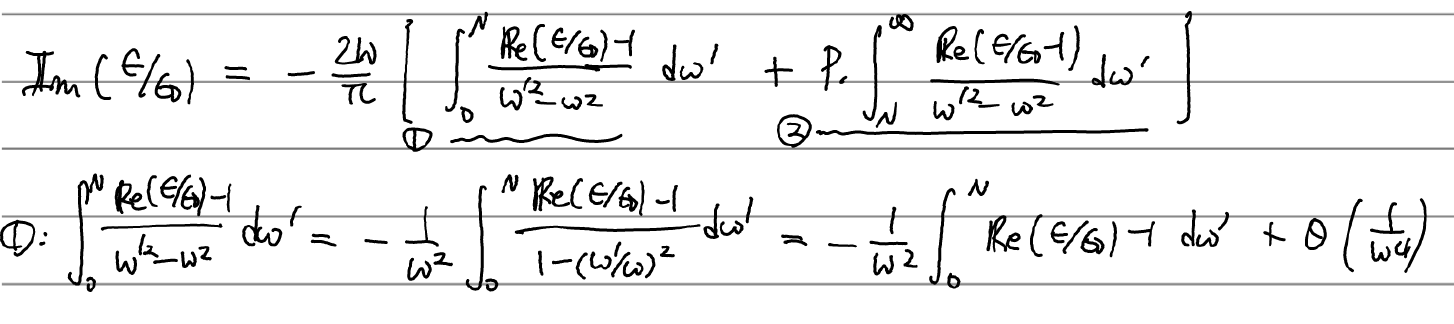
(1)에 P가 없는 이유는 w>N이고, 적분 구간으로부터 w'<N이면 분모가 0이 되는 순간이 없기 때문이다. 둘째줄 두번째 등호는 1/(1-x)=1+x+x^2+.. (x=(w'/w)^2) 이용.

첫 등호는 아까 첨에 썼던 근사식 \( Re(\epsilon/\epsilon_0) -1 = -w_p^2/w^2 + O(1/w^4) \) for w>N 을 대입한것.
두 항을 합치면 유도가 끝났다.
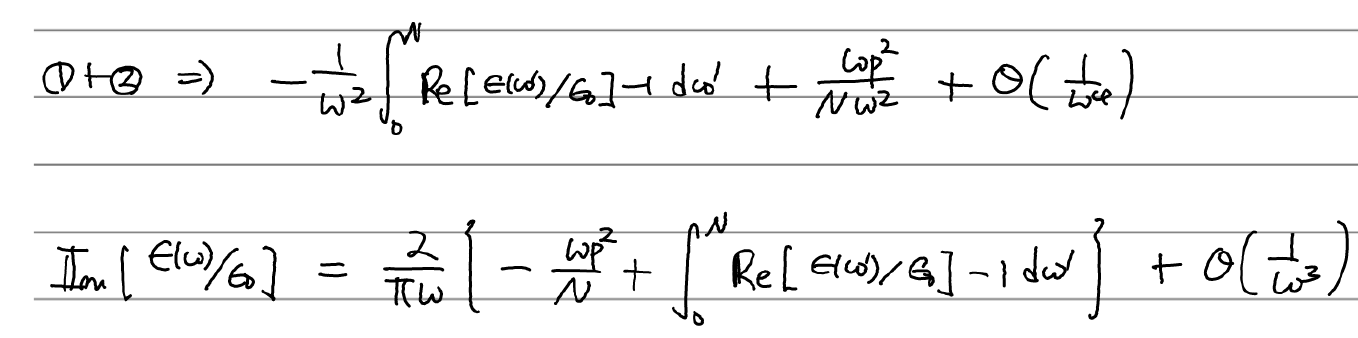
도체에 대해선 두 sum rule이 다음과 같이 바뀐다.

'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 7.9 : 펄스의 분산 (2) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 7.8 : 위상속도와 군속도 (1) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.5 : 유전물질, 도체의 분산관계 (2) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.1~7.4: 전자기파의 도입 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화 (0) | 2024.12.06 |