(작성일: 2024-12-03 15:13)
7.8 Superposition of Waves in One Dimension; Group Velocity
분산적인 매질(dispersive media), 즉 파장에 따라 굴절률이 다른 매질에서 여러 진동수의 단색광이 혼합된 빛이 어떻게 전파되는지 다룰 것이다.
이번 절에서 얻어지는 주요한 세가지 결과는 다음과 같다.
1. 매질이 dispersive하다면, 즉 유전 상수가 장의 진동수의 함수라면, 위상속도는 파동의 각 진동수 성분마다 달라지게 된다. 따라서 파동의 각 진동수 성분은 다른 속도로 진행될 것이며 그 위상 또한 달라지게 될 것이다.
2. dispersive한 매질에서, 에너지 흐름의 속도는 위상속도와 매우 달라지게 될 것이며, 심지어 엄밀한 의미마저 잃게 될 수 있다.
3. dissipative한 매질에서, 복사의 펄스는 진행됨에 따라 감쇠하게 되는데, dissipative 효과가 진동수에 민감하냐 아니냐에 따라 distortion과 함께 감쇠될 수도 distortion 없이 감쇠될 수도 있다.
편의를 위해 1차원 스칼라 파동 u(x,t)를 생각하자. 이는 여러 파장의 파동이 합쳐져 있는 것으로 생각할 수 있다. 수학적으로 말하자면 푸리에 변환이다.
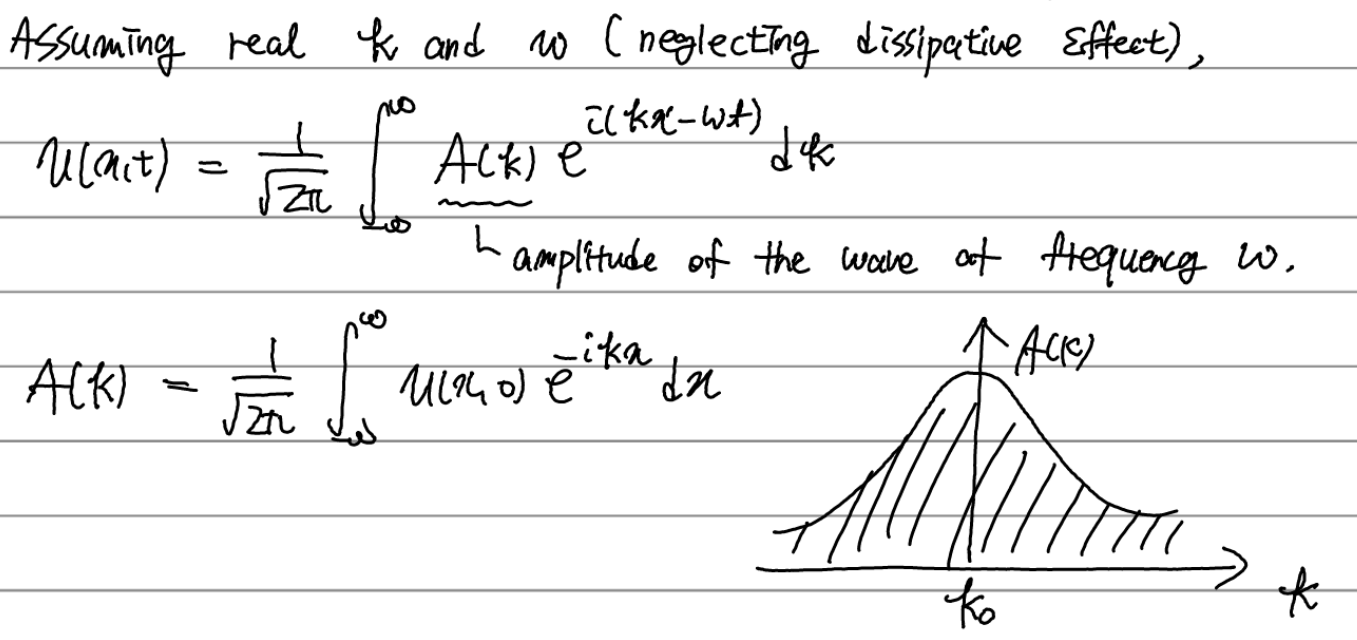
단일 파장의 파동은 다음과 같이 디락델타함수를 이용하여 생각할 수 있다.

파속(wave packet, wave train)에 대해서는 대략 다음과 같은 이야기가 가능하다.

\( \Delta x \)는 공간상에서 파속의 길이(스케일)이고, \(\Delta k\)는 k space에서 나타나는 파속의 길이(스케일)이다. 두 값의 정확한 정의 및 관계는 다음과 같다.

너무 파속이 abrupt하지만 않으면 항상 성립한다.
물리적으로, 여러 파장의 파동이 섞인 파동은 dispersive한 매질을 통과하면 시간이 지날수록 점점 퍼지게 된다. 각 파장별로 매질 속 속도가 다르기 때문이다. synchronized wave는 distort되고 dephasing되는 것이다. 이를 다뤄보기 위해 dispersion relation \(\omega (k) \)를 다루자.
$$ \left. \omega(k) \simeq \omega(k_0) + (k-k_0) \frac{d\omega}{dk} \right|_{k=k_0} + \cdots $$
위와 같은 테일러전개를 하고, 일차항까지만 쓸 것이다. 이 근사 또는 가정은 우리의 파동(이하 pulse)에 섞여있는 단일파장파동들의 파장의 spectrum이 그리 넓지 않고(=wave number의 spectrum이 그리 넓지 않고), w가 k에 weakly depend하고(=고차항의 영향이 거의 없고), amplitude A(k)가 k0에서 sharp한 peak을 가진다는 것을 의미한다.

식의 시각적 표현은 Best explanatory .gif of phase velocity and group velocity I've found so far. Mildly entertaining to watch too, so I thought I'd share. : r/Physics 나 Group velocity - Wikipedia 와 같은 링크의 gif를 참고.
식을 해석하자. t=0일 때의 파속의 전반적인 형태(envelop)는 시간이 흐름에 따라 dw/dk |k_0 (=v_g)의 속도로 진행하고, 동시에 oscillating phase가 붙어 진동한다. (우리가 흔히 파동할 때 떠올리는 sin파는 u(x,t)의 real part만 보는 것임을 상기)
에너지는 장의 진폭과 관련이 있으므로, 에너지는 v_g의 속도로 이동(transport)한다. 에너지의 전달이란 정보의 전달로도 볼 수 있기에(가령 1011.. 같은 이진수를 전송하기 위해 높은 에너지는 1, 낮은 에너지는 0으로 약속하여 에너지를 시간에 따라 바꿔가며 전송하는 상황을 생각해보라), 정보 또한 v_g의 속도로 이동한다. 이것이 군속도의 물리적 의미이다.
이제 빛으로 넘어가서, 위상속도와 군속도를 구해보면 다음과 같다.
$$ \omega(k) = \frac{ck}{n(k)} $$
$$\begin{align} \text{phase velocity : } v_p &= \frac{\omega}{k} =\frac{c}{n} \\ \text{group velocity : } v_g & = \frac{c}{n + \omega \frac{dn}{d\omega} } \end{align}$$
군속도의 유도과정)
$$\begin{align} n\omega = ck \xrightarrow{d/dk} & \frac{dn}{d\omega} \frac{d\omega}{dk} \omega + n\frac{d\omega}{dk} = c \\ \\& \underbrace{\frac{d\omega}{dk}}_{v_g} ( \omega \frac{dn}{d\omega} + n) = c \Rightarrow v_g = \frac{c}{n+\omega (dn/d\omega)} \end{align}$$
군속도에 대한 논의를 좀 더 해보자.

(참고: w0=w(k0)=ck0/n=ck0 (n=1이므로), n=sqrt(eps/eps0) (eps, n both complex number). 좌측 그래프는 n의 real part)
normal dispersion의 경우, dn/dw>0이므로 v_g<c이며 v_g != v_p인것을 볼 수 있다. v_g는 에너지의 이동속도이므로, 광속을 넘지 않는 것을 볼 수 있다. 그러나 anomalous dispersion의 경우, dn/dw<0이며, n<1인 순간도 존재하므로 v_g>c일 수가 있게 된다. 또 dn/dw<<0인 순간에는 v_g<0이 될 수도 있게 된다. v_g가 에너지의 이동속도인데 c보다 커진다면 상대론에 위반되는 거 아니냐 생각이 들 수 있지만, dn/dw가 매우 커진다는 것은 w가 k가 변함에 따라 매우 빠르게 변한다는 것으로, 위에서 테일러 전개의 일차항만 남기는 근사가 더이상 성립하지 않게 되기 때문에 군속도가 에너지의 전달속도랑 일치하지 않게 된다. 또한 빛의 군속도 식 또한 전부 valid하지 않게 된다.
그럼에도 불구하고 anomalous dispersion에서의 군속도가 갖는 의미가 완전히 사라지는 것은 아닌데, 자세한 것은 잭슨 참고. 그치만 중요한 내용은 아니다.
참고로, 위상속도는 빛의 속도를 초과해도 된다. 굴절률이 1 미만인 물질은 많다.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 7.10: 전자기학에서의 인과율, Kramers-Kronig Relations (2) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 7.9 : 펄스의 분산 (2) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.5 : 유전물질, 도체의 분산관계 (2) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.1~7.4: 전자기파의 도입 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화 (0) | 2024.12.06 |