(작성일: 2024-12-03 16:16)
7.9 Illustration of the Spreading of a Pulse as It Propagates in a Dispersive Medium

전에 썼던 u(x,t)와 A(k)의 관계식(=푸리에변환)이다. 어차피 실제 파동은 이것의 real part만 취하므로, u(x,t)를 다음과 같이 쓸 수 있다. Re(e^ix) = cos x = e^ix+e^(-ix)/2

(c.c.는 complex conjugate로, 앞 항에 complex conjugate 취한 항이 뒤에 더해져있음을 말함)
그럼 이것의 inverse transformation 개념으로 다음의 식 또한 유도 가능.

이제 이번 장의 논의를 위해 다음의 특별한 파동을 생각하자.

논의의 편의를 위해 다음을 가정하자.

이에 해당하는 물리적 상황은 다음과 같다. t=0 이전에 두개의 파동이 각각 왼쪽과 오른쪽에서부터 각각 오른쪽과 왼쪽으로 향하도록 진행하다 t=0에서 합쳐졌을 때(superposition) 저런 u(x,0)이 나온 것이다. 시간이 t=0이후로 진행하면 둘은 다시 갈라져 원래 가던 방향으로 나갈것이다.
이 u(x,0)을 위의 A(k)식에 대입.

이제 다음의 dispersion을 가정.

참고로 여기서 v처럼 생긴건 속도가 아니라 \(\nu \), 어떤 constant frequency를 말한다. a는 dispersion의 스케일을 주는 어떤 certain length고 임의로 설정된 값이다. 군속도는 다음과 같다.

이제 u(x,t)를 계산해보면...


가 나온다. 마지막 식은 approximately completing the squares in the exponent 해서 구해진다는데 안해봐서 무슨 말인지 잘 모르겠다. 마지막 식의 꼴을 보면 앞에서 논의한 물리적 상황대로, v_g의 속도로 각각 왼쪽과 오른쪽으로 가는 두개의 파동의 합임을 확인할 수 있다.
envelope의 width는 다음과 같다. (L(t)를 아래처럼 정의해서 위 식이 저렇게 정리된 것)

이로부터 sharper한 pulse일수록 더 큰 dispersive effect가 나타나는 것을 확인할 수 있다. 우선 long time limit에서,

확인을 위해 다음과 같은 두 상황을 생각하자. (1): k0L>>1 (2): k0L < 1 (k0는 pulse의 wavenumber임을 상기)

두 wave packet은 다음과 같이 시간에 따라 진행한다.
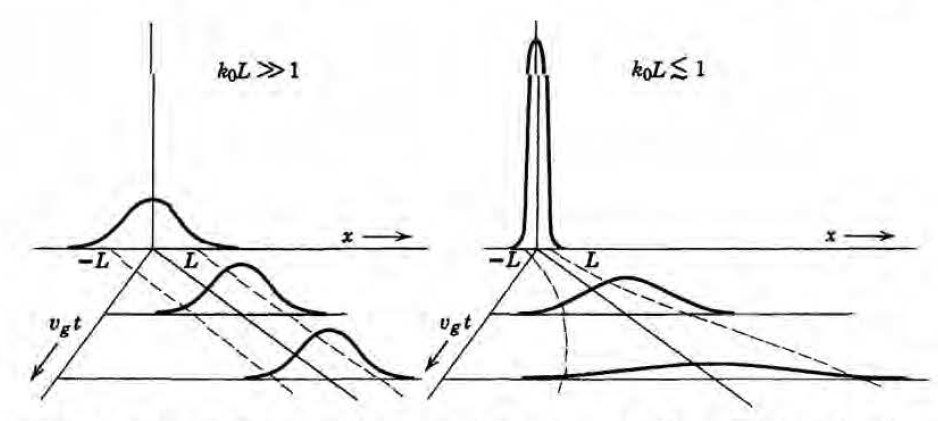

비록 지금까지의 내용이 특별한 파동 하나에 대해 구해졌지만 정성적 논의는 일반적으로 적용된다.
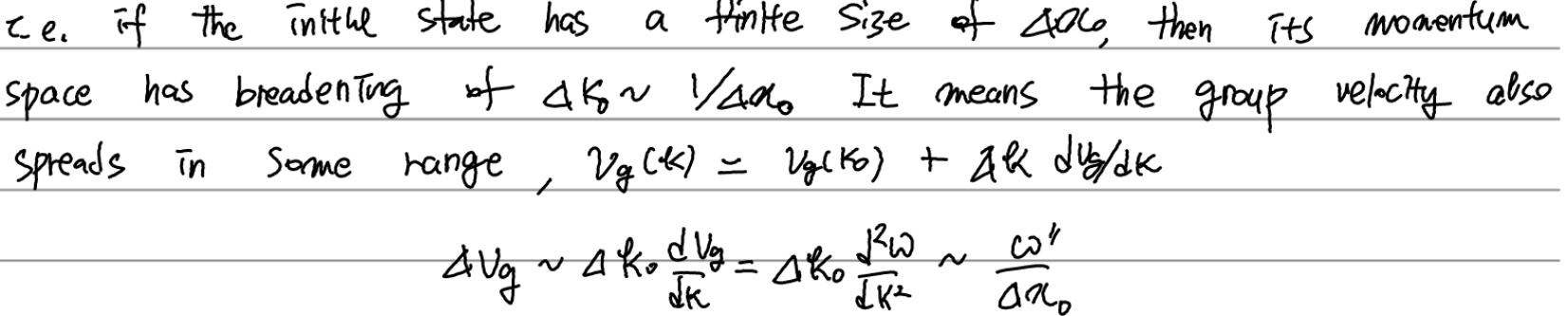
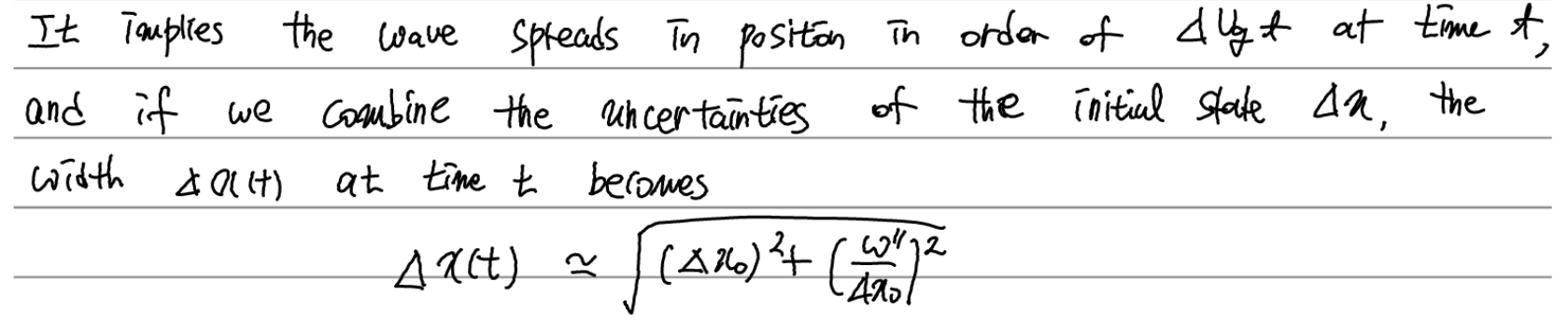
한마디로, 좁은 packet은 시간이 지남에 따라 빠르게 퍼지고, 넓은 packet은 천천히 퍼진다.
양자역학(교재에선 wave mechanics로 언급 )에서도 이러한 현상은 동일하게 나타난다.
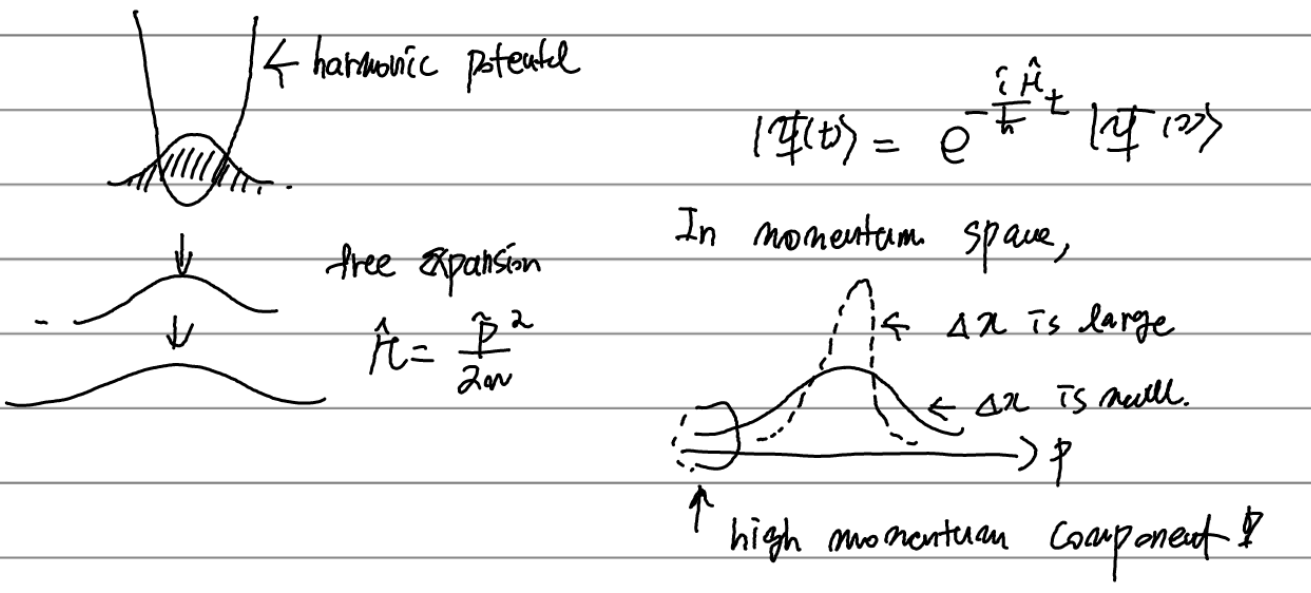
왼쪽의 상황은 harmonic potential에 갇혀있던 wavefunction이 potential을 없애주면 퍼져나가는 상황이다.
마지막으로 잭슨은 wave packet이 dispersive한 매질 속에서 dissipate하는 경우에 대해 얘기하는데, 시간이 지남에 따라 dispersion에 의해 퍼져나가면서 동시에 attenuated되고 distort된다고 한다. 그치만 해석적으로 식을 풀어써서 하는 논의는 특별한 경우를 제외하곤 어려우며, 몇가지 레퍼런스를 소개한다.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 7.10: 전자기학에서의 인과율, Kramers-Kronig Relations (2) | 2024.12.06 |
|---|---|
| [잭슨 전자기학] Ch 7.8 : 위상속도와 군속도 (1) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.5 : 유전물질, 도체의 분산관계 (2) | 2024.12.06 |
| [잭슨 전자기학] Ch 7.1~7.4: 전자기파의 도입 (0) | 2024.12.06 |
| [잭슨 전자기학] Ch 6.11, 6.12: 자기홀극, 디랙 양자화 (0) | 2024.12.06 |