유전물질에서의 경계조건 문제를 풀자.
가장 간단한 상황부터 생각해보자.

왼쪽이 우리가 풀려는 상황이고, 오른쪽은 영상법을 쓰기 위해 image charge를 부여한 상황이다.
기본적으로 우리가 전기장을 구하기 위해 풀어야 하는 방정식은

이고, 경계조건은

이다. 처음 두개는 tangential 방향 전기장에 대한 조건, 마지막 하나는 normal 방향 전기장에 대한 조건. 경계조건 식에 대해선 이전글( [잭슨 전자기학] Bound charge - 속박 전하) 하단을 참고. normal 방향 전기장 조건에 대해 설명하자면 free surface charge가 없는 상황이기 때문이다. 참고로 D=eps0 E + P = eps E이므로 P는 이미 eps에 포함되어 있으니 생각할 필요 없다.
그러나 우린 저 방정식을 그대로 사용하여 전기장을 구하진 않을 거고, 늘 그래왔듯 퍼텐셜을 구한 뒤 미분하여 얻을 것이다. 그리고 그 퍼텐셜은 위 그림 오른쪽에 그렸듯 image charge를 도입하여 영상법을 통해 얻을 것이다.
우선 경계 오른쪽(실제 전하가 있는 쪽, z>0)의 퍼텐셜부터 구해보자. image charge를 놓는 곳은 경계 맞은편, 동일한 거리 d만큼 떨어진 곳이다. 왜? 직접 구해보면 나온다.. 는 너무 당연한 얘기고 정보값도 없는 이야기니 조금더 디테일하게 얘기하자면,

위의 식은 실제 점전하 q에 의해 경계에 유도되는 surface bound charge \( \sigma_b \)를 구해본 것이다. 첫 식의 4번째 등호는 Pz가 아니라 Eztot만을 가리키는 등호. (상황 설명: z축이 오른쪽 방향. 원점은 q에서 경계로 내린 수선의 발. rho는 원통좌표계에서의 \(\rho\)로, \(\sqrt{x^2+y^2}\). 그림이 이래서 그렇지 3차원을 고려하는 중. \( \sigma_b \)는 위치에 따라, 즉 (x,y)에 따라 다름에 유의. 결과적으로 \(\rho=\sqrt{x^2+y^2}\)에 대한 함수로 구해짐) 잘 보면 양변에 sigma_b가 존재한다. 즉 편극 자기 자신이 만드는 전기장이 자신에 미치는 영향이 고려되고 있는 중으로, 4.3, 4.5절에서 논의한 바와 부합하는 부분이다.
여튼 이렇게 구한 surface bound charge를 도체에서의 식과 비교해보면,

계수만 차이가 날 뿐 동일한 꼴( \( \sim d/(\rho^2+d^2)^{3/2} \) )임을 확인 가능하다. 도체에서의 image charge가 놓이는 위치가 경계에서 동일한 거리만큼 떨어진 곳 z=-d임을 생각하면, dielectric에서도 image charge가 놓여야 하는 곳은 z=-d이다.
이제 z>0에서의 퍼텐셜을 구하자. 사실 핵심적인 계산은 다 했다. 실제 점전하 q와, image charge q'이 만드는 퍼텐셜을 더해주면 되는데, 전자는 단순히

로 구해지고, 후자는 image charge

가 만드는 퍼텐셜이므로 (q'이 왜 저렇게 구해지는가: 도체에서의 image charge의 전하량은 -q인데, 도체에서의 sigma_b와 dielectric에서의 sigma_b가 몇 배 차이나는지 확인해보라)

와 같이 구해진다. (사실 지금은 은근슬쩍 \( \epsilon_1 \)이 아니라 \(\epsilon_0 \)일 때에 대해 구했다. 밑에서 경계조건을 이용해 제대로 구할 것.)
후자는 전체 (유도된 속박)면전하가 만드는 퍼텐셜로 보고 계산한 값과도 일치한다. 편극 P가 만드는 퍼텐셜(=속박전하가 만드는 퍼텐셜)은 다음과 같은데,

에서 rho_b=0 (dielectric 내 free volume charge가 없으므로 - [잭슨 전자기학] Bound charge - 속박 전하 하단 참고) 이므로 앞 항만 계산하면 된다. 이는 속박면전하가 만드는 퍼텐셜.
그럼 보다 근본적으로 왜 실제 점전하가 bound volume charge를 유도하지 못하느냐 라는 질문이 들 수도 있는데, 이는 \( P = \epsilon_0 \chi_e E \)가 성립하는 linear dielectric이기 때문이다. 잭슨에도 이에 대한 설명이 있다. \( \rho_b = -\nabla \cdot P = -\epsilon_0 \chi_e \nabla \cdot E =0 \) except point charge q 라는 식으로 설명했는데, \( \nabla cdot E = \rho/\epsilon_0 = (\rho_f+\rho_b)/\epsilon_0 \) 이기 때문에 사실 rho_b가 0이라는 걸 얘기하려면 한번 이항해서 보여주는 과정이 있어야 하긴 한다. surface에 대해선 이 논리가 성립하지 않는데, \chi_e가 경계를 기준으로 바뀌기 때문이다. 그래서 surface bound charge는 0이 아닐 수 있는 것.
이제 dielectric 안, z<0에서의 퍼텐셜도 구해보자. 도체에서와는 달리 0이 아님에 유의. 처음 그림의 우측하단에서처럼 image charge를 z>0에다가 잡아야 하며 그 위치는 z=d여야 한다. image charge는 항상 관심 영역 밖에 둬야 한다! 이유는 ch2 참고.
$$ V = \frac{1}{4 \pi \epsilon_2} \frac{q''}{\sqrt{\rho^2+ (z-d)^2}} \text{ at z<0} $$
이제 경계조건을 적용하여 q'과 q''을 구하고 퍼텐셜을 완성하자.
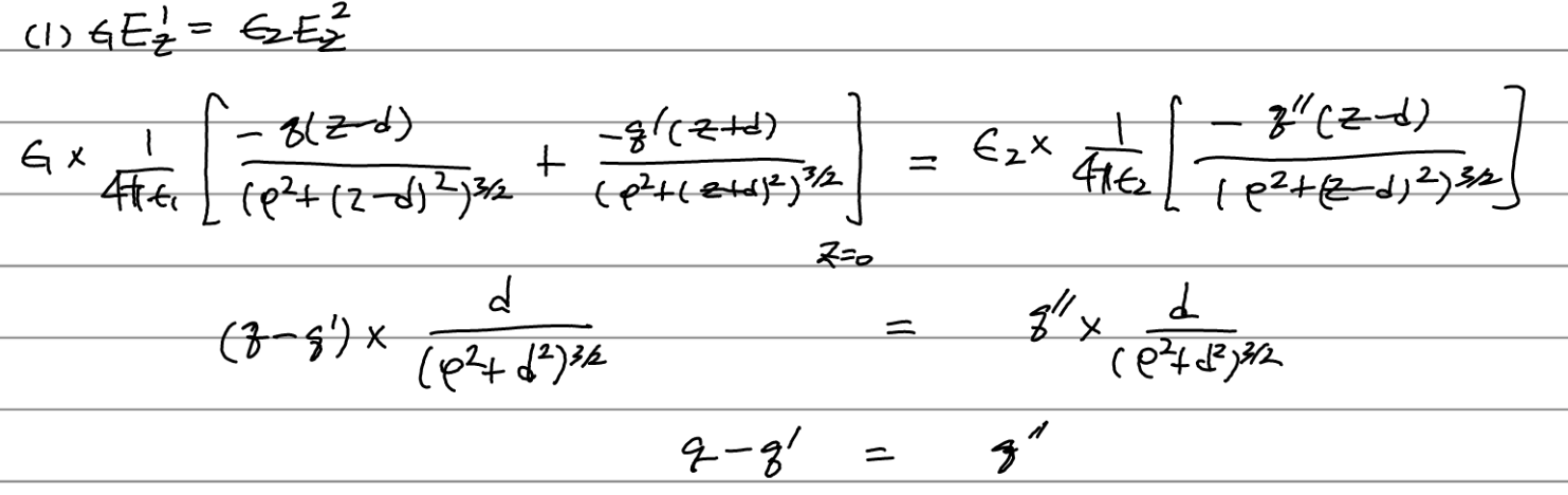


따라서 경계조건을 이용해 image charge q'과 q''을 결정할 수 있었으며, 퍼텐셜은 다음과 같다.
$$ \Phi = \frac{1}{4 \pi \epsilon_1} (\frac{q}{\sqrt{\rho^2+ (z-d)^2}}+\frac{q'}{\sqrt{\rho^2+ (z+d)^2}}) \text{ at z>0} $$
$$ \Phi = \frac{1}{4 \pi \epsilon_2} \frac{q''}{\sqrt{\rho^2+ (z-d)^2}} \text{ at z<0} $$
(분모의 유전율에 유의)
surface charge도 안 구해볼 수 없다. free surface charge가 없으므로 이는 온전히 surface bound charge와 동일하다.

surface에서니 z=0일 때의 Ez를 이용해야 하는 걸 깜빡하지 말기.
도체로의 극한에 대한 논의는 다음과 같다.

교재의 노테이션은 다음과 같다.


약간 신경써야 할 것은 (늘 그렇듯) 부호다. dielectric의 경우 유전율의 대소관계에 따라 image charge가 도체에서처럼 항상 반대부호가 아니라 같은 부호로 나올 수도 있기 때문에 더 주의해야한다.

이런 식으로 생각할 수도 있다.
bound charge sigma_b의 물리적 의미는 다음 그림과 같다.

이런 구성으로 인해 free charge도 없고, 도체판에서처럼 접지되어 있어 외부전하가 공급될 수 있는 환경도 아닌데도 net charge가 경계에 존재할 수 있게 된다.
전기력선을 그려보면 다음과 같다.

z<0 영역에선 전기장을 q'' 혼자 만들기 때문에 z=d로부터 직선으로 뻗어나오는 방향으로 그려지고, z>0 영역에선 q와 q'이 함께 만드는 전기장이 그려지게 되는데 유전율의 대소관계에 따라 q와 q'이 같은 부호가 되기도 다른 부호가 되기도 하기 때문에(참고로 q랑 q''는 항상 같은부호) 저렇게 그려진다. 같은 부호가 될 때가 오른쪽, 다른 부호가 될 때가 왼쪽 그림이다. 이런 식으로 생각하면 볼록하게 휘도록 그려야 하는지 오목하게 휘도록 그려야하는지 헷갈리지 않을 수 있다.
교재에선 또 하나의 예시를 소개한다. dielectric sphere 외부에 전기장을 걸어주는 예시이다. 그러나 3장에서 풀던 boundary problem과 boundary condition만 바뀌었을뿐 본질적으로 동일하기 때문에 생략하겠다. (접근법만 간단히 얘기하자면, 외부 전기장에 평행한 방향을 z축으로 잡으면 계가 z축 원통 대칭성이 생기기 때문에 퍼텐셜을 sum (Ar^l+Br^-l-1)Pl(cos theta) 꼴로 잡고 풀 수 있다)
dielectric 내 dipole이 전기장을 상쇄시키는 방향으로 유도되기 때문에 전기장 크기가 줄어든다거나, 구 내부 유전율을 eps0으로 두고 구 밖 유전율을 eps로 두면 dielectric cavity로 생각할수도 있다던가 하는 논의들이 있으나 이 역시 뻔한 얘기들이니 생략한다.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 5.5: 정자기학(2) - 고리 전류가 만드는 자기장과 벡터퍼텐셜 (0) | 2024.11.13 |
|---|---|
| [잭슨 전자기학] Ch 5.1~5.4 : 정자기학(1) 비오-사바르 법칙, 앙페르 법칙, 벡터 퍼텐셜 (0) | 2024.11.05 |
| [잭슨 전자기학] Bound charge - 속박 전하 (0) | 2024.10.13 |
| [잭슨 전자기학] Ch 4.6 (0) | 2024.10.13 |
| [잭슨 전자기학] Ch 4.5 (0) | 2024.10.12 |