bound charge를 잭슨에서는 polarization-surface-charge, polarization-charge density라는 이름으로 부르나, 그리피스만큼 명확히 정의하고 비중을 크게 두어 boundary problem을 푸는 과정에서 적극적으로 이용하지는 않는다. 다만 4.3절에서 (※) 표시를 해둔 부분과 같이 빼놓을 수 없는 내용이다. 그리피스와 비교해가며 설명해보도록 하겠다.
부피 V 내에 있는 편극 P(r')가 만드는 퍼텐셜은 다음과 같다. (즉 부피 V도 P도 퍼텐셜 V도 전부 macroscopical - 잭슨에서의 유도와 조금 출발점이 다르다.)

정리하면
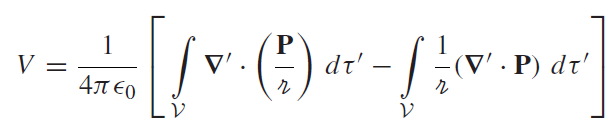

잭슨에선 나오지 않았던 surface term이 나왔다. 이는 두 책의 상황이 다르기 때문일까?
잭슨 : (4.30)식의 \(\Delta V\)라는 영역은 macroscopic하게는 x'이라는 한 점으로 표현되는, macroscopically small but microscopically large region이었다. 즉 \( \Delta V = d^3 x' \)인 셈이다. \( \Delta P(x') \)은 macroscopic한 parameter로 \( \Delta V\)라는 영역 전체를 대표하는 편극 값을 말한다. \(\Phi(x)\)를 유도할 때 들어간 적분기호는 macroscopically "large"한 source를 다루겠다는 것이다.
그리피스: 부피 V는 macroscopic하게 수많은 점을 포함하는 부피영역이다. 즉 macroscopically "large" 영역이다.
즉 적분기호가 들어간 식부터는 잭슨과 그리피스가 다루는 상황이 동일하며, 잭슨의 surface term 생략은 잘못되었다! (그럼에도 뒤에서 D를 정의하고 논리를 전개하는데 문제가 없는 이유는 가우스 법칙이 surface를 무시하기 때문이다.)
이제 다음을 정의하자. 이 둘을 bound charge(속박전하-말그대로 원자나 분자 내에 속박되어 이동하지 못하는 전하)라고 한다.
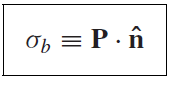
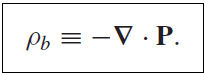
그럼 다음과 같이 쓸 수 있다.

즉 편극 P가 만드는 퍼텐셜은 면전하(밀도) \( \sigma_b\)와 부피전하(밀도) \( -\nabla \cdot P\)가 만드는 퍼텐셜의 합이다. 이는 우연의 일치가 아니며, 그리피스 4.2.2에서 편극 P를 이 면전하와 부피전하의 합으로 생각할 수 있는 물리적 이유에 대해 논의한다. 여기선 생략.
이제 매질(참고로 잭슨 4.3절에서 가정한 이상적인 dielectric, 유전물질을 말하는것)에서의 가우스법칙을 다시 보자.
매질 내의 총 부피전하밀도는 다음과 같이 쓸 수 있다.

\(\rho_f\)는 free charge(자유전하)로, bound charge 외의 이동할 수 있는 모든 전하를 말한다.
그럼 가우스 법칙은

으로 쓰인다. (이때의 전기장 E는 편극 P에 의해 만들어진 전기장 뿐만 아니라 다른 모든 전기장(외부 전기장 등)을 포함하는 macroscopic한 전기장) 따라서



가 된다. 즉 잭슨의 식에선 \(\rho_f\)를 \( \rho \)로 표기했던 것. 이건

이 식부터가 rho와 P를 따로 써주었으니 P에서 나오는 bound charge가 rho에 포함되지 않는다는 사실로부터도 확인가능.
잭슨에서 surface term을 무시했던 것은 D를 유도하는 과정에서 쓰인 가우스법칙이 surface를 무시하기 때문에 가능했던 거였다.
경계조건에 대한 이야기를 하자.
잭슨 4.3절에선 유도없이 다음과 같이 쓰고 넘어갔다.

이를 그리피스에선 좀더 보기 쉽게 나눠 써놨다.
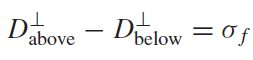



옆으로 나열한 식끼린 동치인 식. 잭슨의 첫식에 있는 \( \sigma\)는 그리피스 식의 \(\sigma_f\)와 같다는 것을 상기하자.
잭슨의 두번째 식은 \( (\mathbf{E}_2^{\perp} + \mathbf{E}_2^{\parallel}-\mathbf{E}_1^{\perp} - \mathbf{E}_1^{\parallel}) \times \mathbf{n}_{21} = \mathbf{E}_2^{\parallel}- \mathbf{E}_1^{\parallel} =0\)으로, 그리피스의 두번째 식과 같은 식이다.
참고로, volume bound charge는 dielectric 내에 free charge가 직접 들어있지 않는 이상 0이다. 고로 \( \rho=\rho_f+\rho_b \) 또한 0. 다음의 그리피스 설명 참고.

여기까지 bound charge 및 경계조건에 대해 짚어보았다. 이제 잭슨 4.4절에 들어가자.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 5.1~5.4 : 정자기학(1) 비오-사바르 법칙, 앙페르 법칙, 벡터 퍼텐셜 (0) | 2024.11.05 |
|---|---|
| [잭슨 전자기학] Ch 4.4 Boundary-Value Problems with Dielectrics (0) | 2024.11.02 |
| [잭슨 전자기학] Ch 4.6 (0) | 2024.10.13 |
| [잭슨 전자기학] Ch 4.5 (0) | 2024.10.12 |
| [잭슨 전자기학] Ch 4.3 (0) | 2024.10.12 |