4.6 Models for the Molecular Polarizability
원자 또는 분자의 '집단적' 분극이 일어나는데는 2가지 가능성이 있다.
1) 인가된 전기장에 의해 쌍극자가 유도(induced dipole moment)되어 발생. 참고로 이런 현상은 분자뿐만 아니라 중성원자에서도 일어날 수 있다.
2) 랜덤한 방향을 향하는 이미 분극되어 있는 분자들이 인가된 전기장에 의해 정렬되면서 발생
1)은 harmonically bound charge를 가정. 전기장에 의해 평형 상태에서 전하가 x만큼 떨어졌을 때(즉 유도된 쌍극자의 +전하와 -전하가 떨어진 거리가 x) 받는 힘이 다음과 같다는 소리다.
$$ \vec{F} = - m\omega_0^2 \vec{x} $$
$$ m\omega_0^2 \vec{x} = e\vec{E} $$
즉 다음이 성립한다.
$$\vec{p}_{mol} = e \vec{x} = \frac{e^2}{m\omega_0^2} \vec{E} $$
$$ \gamma = \frac{e^2}{m \omega_0^2 \epsilon_0} $$
$$ \gamma_{mol} = \frac{1}{\epsilon_0} \sum_j \frac{e_j^2}{m_j \omega_j^2} $$
사실 마지막 식은 뭘 가리키는지 잘 모르겠다. gamma가 여러 분자들을 합쳐서 생각해도 되는건가.. 분자 종류 j별 개수는 고려안해도 되는건가..
뒤에선 스케일에 대한 이야기가 나온다. gamma는 부피 차원이므로 우선 분자의 부피 정도의 값으로 추측해볼수 있다. 원자 하나 크기가 대충 10^-10~-9m 정도이므로 세제곱하면

\( \gamma = e^2/m\omega_0^2 \epsilon_0 \)을 이용해서도 스케일을 추정해보자. omega는 binding frequencies of electrons in atom으로, 빛의 진동수로 생각할 수 있다. typical한 값인 3000옹스트롬을 대입하여 구하면

로, 두 추정치가 일치하는 걸 확인할 수 있다.
4.5절에서 구한 \( \gamma \)와 \( \chi_e \)의 관계식을 이용하여 \( \chi_e \)의 추정치도 구해서 (이 때 N은 NTP 조건(1기압, 0도씨)에서 기체의 단위부피당 분자 수 2.7 * 10^25를 이용) 유전율을 구해보면 실험값과도 스케일이 맞는 것을 확인할 수 있다. 액체나 고체처럼 N이 큰 경우에도 이는 성립한다.
\( \gamma = e^2/m\omega_0^2 \epsilon_0 \) 라는 공식이 열에 의한 교란(thermal agitation)에 의해 변경될 가능성은 없을까? 이를 다루기 위해 통계역학(...)을 이용하자. 위상공간(phase space)에서 입자가 (p,q)에 위치할 확률분포는 hamiltonian H=H(p,q)에 대한 함수 f(H)로 나타낼 수 있으며, 고전적인 계에서는 볼츠만 분포를 따르므로 \( f(H)= e^{-H/kT} \)이다.
전기장이 z축 방향이라 가정하자. \( \bf{p} \)는 charged particle(원자 또는 분자)의 momentum이다.

그럼 z축 방향 dipole moment의 평균값은 다음과 같이 계산할 수 있다. 확률분포로 기댓값을 계산하는 고등학교 통계지식 이용.

사소한 두가지 의문이 들 수 있다.
(1) z축 방향 dipole moment를 ez로 계산하는게 맞느냐, 그러니까 p=qd에서 q는 e일수밖에 없겠지만, (유도된) 쌍극자의 두 전하의 간격을 z로 표현하는게 맞느냐: 해밀토니안으로 돌아가보면 마지막 항이 -eEz다. 에너지가 qV=qEd로 구해지는 걸 생각해보면, z는 정확히 쌍극자의 두 전하의 간격을 의미한다.
(2) <p_mol>을 계산하는데 사용되는 확률분포가 f(H)가 되는게 맞느냐: 통계지식을 떠올려보자. 확률변수 X의 확률밀도함수가 f라고 하면 확률변수 Y=g(X)의 기댓값을 구할시 f를 사용하여 구할 수 있다. f(H)는 '계가 (p,q)로 표현되는 상태에 있을 것이냐'에 대한확률밀도함수고, p_mol은 계가 어떤 상황이냐에 의존한다. 따라서 문제 없음.

로 좌표변환을 해주면,

가 되고, (마지막항이 더이상 z를 포함하지 않고 상수가 된것을 확인하라)

가 되어 계산하기 편해진다.
분모는 1이고, 분자의 첫항은 z'이 odd function이므로 적분하면 0이되고, 뒷항은 상수를 적분 밖으로 전부 빼내고나면 적분값이 1이 나오므로

가 나온다. 이는 기존의 식과 동일하므로, 열적 교란은 기댓값에 영향을 주지 않는다.
이제 2)번 케이스를 고려하자. H2O나 HCl 같은 극성분자들이 매질을 구성하는 경우가 해당 예시가 되겠다. 매질을 구성하는 분자들이 전부 permanent dipole moment를 지녔다 가정하자. 만약 전기장을 안 걸어줬다면 열적 교란에 의해 각 분자들의 dipole moment가 랜덤한 방향을 향할 것이고 총 net dipole moment는 0이었을 것이다. 그러나 전기장을 걸어준다면 계의 에너지를 최소화하기 위해 분자들이 정렬하게 되면서 net dipole moment가 생기게 될 것이다.
계의 해밀토니안을 다음과 같이 쓰자. H0는 x, p에 의존하지 않고 오로지 분자의 internal coordinates에만 의존하는 부분이다.

이를 위의 <p_mol> 식에 대입하고 정리하면 다음을 얻는다. 이번에도 전기장을 z축 방향으로 둔다. 그러면 p0와의 각도는 theta가 된다. exp(-H0/kT) 부분은 적분기호 밖으로 빼낼수 있기에 분모와 분자의 것이 약분되어 사라지게 된다. int d^3x int d^3p가 int d Omega로 바뀔 수 있는 이유는 잘 모르겠다..

p0E/kT는 극저온만 아니면 1보다 매우 작은 값이기 때문에 exp항을 테일러 전개할 수 있고, 일차항까지만 전개하고 적분을 계산해주고 정리해주면 다음을 얻는다. 보이기 쉬움. 참고로 분모는 1차항을 무시하는 근사까지 해주면 편함.

정리하자면, 1)의 induced dipole moment는

으로 온도에 대해 상수이고, 2)의 경우에는

으로 온도에 대한 함수이다. 그럼 왜 온도가 증가하면 polarizability of permanent dipole moment가 감소할까? 온도가 증가하면 열적에너지로 인해 분자가 더 빠르게 진동하게 되면서 전기장에 의해 정렬되기 어려워지기 때문이다. Problem 15 Explain why the dielectric const... [FREE SOLUTION] | Vaia
1)과 2) 두 요소를 합쳐서 쓴 gamma는 다음과 같고, 이에 대한 실험 결과는 그림 4.10 참고. 온도를 바꿔가며 실험하여 1)과 2) 두 요소를 실험적으로 구분해낼 수 있다.
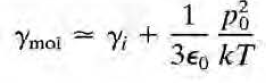
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 4.4 Boundary-Value Problems with Dielectrics (0) | 2024.11.02 |
|---|---|
| [잭슨 전자기학] Bound charge - 속박 전하 (0) | 2024.10.13 |
| [잭슨 전자기학] Ch 4.5 (0) | 2024.10.12 |
| [잭슨 전자기학] Ch 4.3 (0) | 2024.10.12 |
| [잭슨 전자기학] Ch 4.2 (0) | 2024.10.11 |