3.12, 3.13 절을 다루겠다.
3.12 Eigenfunction Expansions for Green Functions

위와같은 \(\psi(x)\)에 대한 미분방정식을 생각하자. (이런 꼴의 미방을 elliptic differential equation라고 함-근데 내가 알기론 더 general한 용어 아니었나 싶긴한데;) (이런 꼴의 미방은 파동방정식, 슈뢰딩거방정식, 푸아송방정식 등 여러가지가 존재)
\( \lambda \)가 특별한 값을 가질 때를 제외하곤 well-behaved(finite&continuous)한 psi(x)를 얻을 수 없다.
그 특별한 값들을 eigenvalue라 하고, 이때의 \(\psi(x)\)를 eigenfunction이라 한다.
왜 선형대수학의 용어가 등장하느냐,
$$ \left[ \nabla^2 + f(x) \right] \psi(x) = - \lambda \psi(x) $$
로, 고윳값문제의 꼴이기 때문. 마찬가지로, 애초에 람다가 고윳값이 아니면 애초에 psi(x)가 나오지 않을 것 같아보이기도 한다. 함수공간은 무한차원이니 억지로 비틀어서 뭔가 나올수도 있어보이는거지..
암튼 고윳값들에 인덱스 n을 붙여서
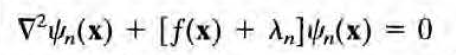
와 같이 쓰고 나면, \( psi_n(x) \)들 간에 다음의 직교성이 성립한다. (eigenfunction들을 normalize한 상태)

고윳값의 스펙트럼은 discrete할수도 있고(=인덱스 n이 countable), contiuous할수도 있고, 둘 다일수도 있다(아마 띄엄띄엄있다가 어느순간 연속적이고.. 뭐 이런걸 말하는거 같음).
고유함수들이 complete set을 이룬다고 가정.
이제 다음을 만족하는 그린함수 G를 찾아보자. 이때 \( \lambda \)는 고윳값이 아님. 그리고 경계조건까지 있다고 하자.

고유함수가 complete set을 이루므로 G를 다음과 같이 전개 가능.

이를 미방에 대입하면 다음을 얻음. 위에서 고유함수 \psi_n(x)가 미방에 들어간 식을 이용한다.

이제 직교성을 이용하여 다음을 얻을수 있다. (양변에 \( \psi_n*(x) \) 곱하고 적분)
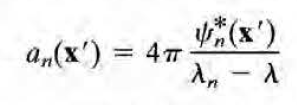
따라서 G는 다음과 같다. n이 continuous하면 sum이 integral로 바뀜.

이제 푸아송 방정식에 적용해보자.

푸아송 방정식은 여기서 f(x)=0, \lambda=0인 케이스이다. 그러므로 고유함수를 구하려면
$$ \nabla^2 \psi_n(x) + \lambda_n \psi_n(x) = 0$$
을 풀어야 한다. 이제 가능한 고윳값을 찾아야 하는데, 이런 꼴의 방정식 중 우리가 알고있는 방정식이 있다. 바로 파동방정식이다.
고윳값을 k^2이라는 연속스펙트럼을 가지는 값으로 두면 고유함수에 대한 방정식은 다음과 같다.

그리고 해도 이미 알고 있다. 앞의 계수는 normalization을 위해 붙음.

이제 이를 그린함수 공식에 대입하여 그린함수 G를 얻어보면 다음과 같다.

이는 1/|x-x'|의 3차원 푸리에 변환이기도 하다. 다소 싱거운 예시였다.
이제 본격적으로 다음 상황에서의 그린함수를 구해보자.

경계조건은 디리클레 조건, 푸아송방정식이다.
위에서와 같은 방식으로 고유값 문제는 다음으로 바뀐다.

디리클레 조건이므로 그린함수는 표면에서 0이 되어야 하고, 따라서 그린함수의 basis가 될 고유함수들도 표면에서 0이 되어야 한다. 미방을 풀기위해 변수분리를 하고 경계조건을 가해주면 다음을 얻는다.


이를 그린함수 공식에 대입하면 다음을 얻는다.

이 식 뒤에 나오는 잭슨의 말이 도통 이해하기 어려운데 무슨 얘기냐 하면 결국 이 식과 동일하나 다른 꼴로 쓰인 그린함수를 찾겠다는 이야기이다. 그리고 그 꼴의 형태는 (3.125), (3.148)과 같은 형태, 가령 (3.125)를 예로 들면

x=(r,theta, phi), x'=(r', theta', phi')이 있을 때 (3.125) 식의 형태는 theta, phi, theta', phi'은 orthogonality를 만족하는 함수 안에 들어가 있고, r과 r'은 둘 중 뭐가 크고 뭐가 작냐 비교한 뒤 r>과 r<의 형태로, orthogonal function의 계수를 이루는 것마냥 들어가 있는 형태다. 그리고 잭슨이 하고 싶어하는 것은 (3.167)의 G(x,x') 또한 형태로(x,y가 theta,phi마냥 orthogonality를 만족하는 함수안에 들어가 있고, z가 r마냥 z>, z< 의 형태로 들어가는 형태)표현하고 싶은 것이다. 이게 본문의 직역(?)이고, 의역(?)을 하여 좀 더 명확히 의도를 쓰자면, 지금 3.12절에서 설명한 그린함수를 구하는 법(미분방정식의 연산자의 고유함수를 구해 기저로 삼아 표현)과 기존에 3.9, 3.11절에서 설명한 그린함수를 구하는 법(해당 좌표계에서 유용한 직교함수를 기저로 삼아 표현)이 같은 결과를 주는지를 기존의 방법으로 이 직육면체 상황의 그린함수를 구해 비교하여 확인하겠다는 것이다.
아무튼 그래서 그 결과는 다음과 같다.


잭슨은 (3.168)의 유도를 스킵했지만, 그리 간단하지 않다.
우선 sin 함수들이 complete set을 이루는 것을 이용하여 그린함수를 다음과 같이 전개한다. 즉 g_n(z,z')이 basis function의 계수인 셈이다.

(이것도 좀 잘못 쓴거 같긴 하다. g_n을 아예 처음부터 g_lmn으로 쓰는게 맞다. 나중에 의존성이 들어가는게 확인되기도 하고, 저렇게 쓰면 sum_n을 뒤로 빼와서 따로 써주면 g_new = sum_n g_n으로 써버릴수도 있기 때문)
이 그린함수를 다음에 대입(참고로 경계조건은 나중에 계수 역할을 하는 g_n에다가 직접 넣어줄 것)
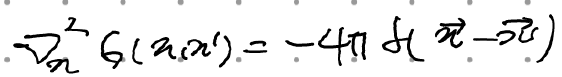
다음을 얻는다.


를 정의하고, g_n의 표기를 다음과 같이 고친다(상수에 l,m 의존성이 들어가버렸으므로)

위의 g에 대한 미방을 풀면 다음을 얻는다.

이제 케이스를 나눈다: z>z'인 경우와 z<z'인 경우로.
3.9절에서 했던 논리를 동일하게 따라가면 다음을 얻을 수 있다. ( Ch3 - (2/4) (tistory.com)의 [(1) 경계조건을 위의 g_l 식에 대입] 부분 참고)

이제 남은건 dg/dz의 discontinuity를 이용해 A를 결정하는 것 뿐이다.

위 식은 처음 g_n이 만족시키는 미방을 z-에서 z+까지 적분함으로써 나온다. 이제 여기에 g를 대입하면,

따라서 전체 그린함수 G(x,x')는

가 되며, 이로써 (3.168)을 보였다.
3.13 Mixed Boundary Conditions; Conducting Plane with a Circular Hole
디리클레 조건과 노이만 조건을 유도하는 과정에서 논의했듯, 두 조건은 퍼텐셜을 unique하게 결정할 수 있는 충분조건이지, 필요충분조건이 아니다. 따라서 두 조건 중 하나에 해당되지 않더라도 퍼텐셜을 unique하게 결정되는 경우가 있을 수 있다. 이번 절에서 살펴볼 예시는 경계의 일부에는 디리클레 조건을, 나머지 영역에는 노이만조건을 주는 경우이다.

z=0에 무한하고 얇고 접지된 도체판을 가운데에 구멍을 뚫어놓은채로 배치해놨다. z->inf에선 크기가 E0, z->-inf에선 크기가 E1인 전기장을 -z방향으로 걸어주는 상황이다.
너무 작위적인 상황은 아니라고 부연설명이 달려있다(waveguide의 벽면에 아주 작은(파장보다 작은) 구멍이 뚫려있어 그 밖으로 radiation이 일어나는 현실적인 상황을 상상할 수 있는데, 이는 위 상황에 0나 E1 중 하나가 0인 상황이라는 것이다)
우선 퍼텐셜을 다음과 같이 쓸 수 있다.
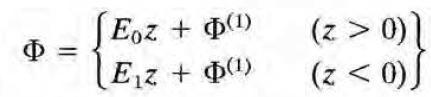
Phi(1)은 도체면의 surface charge로부터 만들어지는 퍼텐셜. 면이 z'=0에 있으므로 다음과 같이 쓸 수 있다.

z를 -z로 바꿔도 Phi(1)은 동일 (even in z)하므로 Ex(1)(x,y,z) = Ex(1)(x,y,-z)=E_x^total (x,y,-z) (외부전기장이 z방향이라서, dPhi/dx = dPhi(1)/dx라서), Ex(1)(x,y,z) = Ex(1)(x,y,-z) =E_y{tot}(x,y,-z).
그러나 Ez(1)은 odd in z \( \Phi(z)=\Phi(-z), d\Phi (z)/dz |_{z=a}= d\Phi(-z)/dz |_{z=a} = - d\Phi(-z)/d(-z) |_{z=-a} = -d\Phi(z)/dz |_{z=-a} \) 인데다 Ez(1) != Ez tot => z=0에서 Ez는 nonzero, rather discontinuous.
이제 경계조건 넣기 시작
(1) 0<= rho <a 에서의 z방향 전기장. z=0에서 continuous해야하므로 등호가 성립.


(2) 금속 판이 접지되어있으므로
$$ \Phi^{(1)} (x,y,0) = 0 \text{ (}a \leq \rho \text{ )} $$
원통대칭성이 있는 계이므로 원통좌표계에서 퍼텐셜의 일반식을 쓰자. 경계조건이 주어진 꼴로부터 다음과 같이 쓸 수 있다. (3.8절 참고)

z>0일 때 식이고, 퍼텐셜이 z에 대해 even이므로 z<0일 땐 z를 -z로 고쳐주면 된다. 그리고 (1) 빠뜨림; (아예 z를 |z|로 고쳐도 됨)
원통대칭성이 있으므로 이 퍼텐셜은 phi에 의존하지 말아야한다. 따라서 m=0인 경우에 해당하고,

이 된다. (A(k)는 교재의 표기인데, 위의 Am(k)랑은 상관 없고 오히려 B0(k)과 같다)
이제 여기에 위의 (1), (2) 조건을 대입해주면 다음을 얻는다.

이 연립적분방정식으로부터 A(k)를 구해야한다. 숨이 턱 막힌다. 이것이 mixed boundary condition을 학생들보고 잘 풀게끔하지 않는 이유이다. 안풀리는 경우들이 있으니까! 첫번째 적분방정식과 두번째 적분방정식이 각각 전체 범위의 일부와 나머지를 커버하는 한 쌍의 적분방정식을 dual integral equations라고 부르는데, 이들은 대개의 경우 복잡하고, 푸는 방법이 잘 연구되어있지 않다. 그래도 지금 우리가 마주한 방정식은 풀이가 알려져있다. 이것이 잭슨이 이 예시를 소개할 수 있는 이유겠지..

와 같은 dual integral equations에서 g(y)는 다음과 같다. 자세한 풀이가 궁금하면 잭슨에 레퍼런스가 있으니 참고.

우리의 방정식은 여기서 n=0, x=rho/a, y=ka를 대입한 상황이다. 따라서 A(k)는..?을 바로 써봤자 감마함수와 구면베셀함수의 덩어리로부터 인사이트를 얻긴 힘들어보인다. n=0이니 사실 구면베셀만 있긴 하지만 우린 일반적인 접근법과 함의를 배우고 싶으니 다음을 먼저 생각해보자.
우리가 관심있는 영역은 아무래도 hole 근처일 것이다. hole에서 너무 멀리 떨어지면 무한 도체판이 있는 상황과 거의 다르지 않으니 말이다. 즉 rho 및 |z|가 너무 크지 않은 영역이 우리의 관심 영역이고, 따라서 그 영역에서의 위에서 구한 퍼텐셜

의 asymptotic behavior을 생각해보도록 하자. J0(k rho)는 베셀함수이므로 rho가 클수록 rapid oscillation을 한다. (그래프를 찾아보고 오면 좋다) exp(-k|z|)는 |z|가 클수록 rapdid decaying을 한다. 즉 A(k)에 곱해진 두 함수 모두 hole과 멀리 떨어진 영역에서는 적분에 거의 기여를 하지 않게 된다. 따라서 적분은 k=0 근처에서 대부분의 기여를 얻게 되고, 우리는 A(k)를 k=0에서 테일러 전개해서 분석했을 때 뭔가 유용한 결과를 얻을 것을 기대할 수 있다. (당연하게도 A(k)가 테일러 전개가 된다는 가정은 깔고가는것)

로 전개하고, 이를 퍼텐셜 식에 대입하면


로 정리할 수 있다. B_l은 다음처럼 정리할 수 있고(파인만의 적분트릭)

문제 3.16c에서 뒤의 적분을 계산해봤으므로 이를 대입하면 다음을 얻는다. (예전에 본인이 수리물리 과제로 풀때는 아마 라플라스 변환을 이용했던거 같고, complex analysis - Laplace transform of the Bessel function of the first kind - Mathematics Stack Exchange 와 같이 contour 적분을 통해서도 계산 가능하다. 잭슨 문제에서 말한 접근은 잘 떠오르진 않는데 아시는 분은 댓 부탁)

어디서 본 듯한 생각이 들었다면 굿.

임을 생각하면, B_l은 르장드르 다항식의 정의를 이용하여 최종적으로 다음과 같이 정리된다.

즉 퍼텐셜은

이 된다.
이제 관찰을 해보자. sum 안에 있는 식마다의 의미를 고찰하자는 것이다. l=0 항은 1/r에 비례하고, l=1 항은 1/r^2에 비례하고, ... 뭔가 학부 때 배운 기억이 나지 않는가? 이건 multipole expansion이다! 즉 A(0)은 total charge (divided by 4pieps0), dA(0)/dk는 dipole moment in z-direction, .. 으로 해석할 수 있다. 이제 A(k)를 다시 볼 때가 왔다. A(k)를 공식으로 마저 계산해주고 구면 베셀함수 j_1의 닫힌 꼴을 대입해주면 다음과 같다.

이를 small k에서 전개해주면

이고, mulitpole expansion의 해석을 적용해보면 leading term(l=1)

$$ \left. \frac{d}{dk} \left( \frac{(E_0 - E_1)a^2 }{3 \pi} \cdot ka \right) \right|_{k=0} \frac{P_1(|\cos{\theta}|)}{r^2} = \frac{(E_0 - E_1)a^2 }{3 \pi} \frac{|z/r|}{r^2} = \frac{(E_0 - E_1)a^2 }{3 \pi} \frac{|z|}{r^3} $$
은 dipole로 해석할 수 있다. 1/r^2 (멀리서는 z~r이므로) 에 비례하는 것으로 다시 한번 확인 가능하다. 이 effective dipole의 dipole moment는

와 같고, 판 위냐 아래냐에 따라 p의 부호가 바뀌는 이유는 수식적으로는 |z|의 미분이 들어가기 때문이고, 실제 dipole이 만드는 퍼텐셜은 odd in z이지만 우리의 퍼텐셜은 even in z이기 때문이다.
이로부터 얻을 수 있는 함의는 전도성 판에 뚫린 구멍은 멀리서 봤을 땐 판의 면에 수직 방향으로 놓인 쌍극자처럼 행동한다는 것이다. 이러한 관찰은 waveguide나 cavity에서 내부의 전자기파가 wall의 구멍 등의 결함으로부터 어떤 영향을 받을지 논의할 때 매우 중요하게 쓰인다.
물리적으로 논의할 것은 다 다뤘다. 이제 계산을 끝내자.

이었고, 적분을 계산해주면(계산 방법에 대한 설명은 잭슨에 나와있다)


이 나온다. 일반해는 알아봤으니 두가지 특수한 케이스에 대해 다루자.
(1) rho = 0 (축 위)

|z|>>a에서 (즉 |z| -> r에서) 식의 값이 0으로 가는 걸 볼 수 있는데, 이는 위에서 구한 쌍극자 형태의 \( \Phi^{(1)} \)의 leading term이 0으로 가는 것과도 일치한다. 또, |z|->0에서는 뒷항이 0으로 가서 첫 항만 남게 되는 것도 볼 수 있다.
(2) z=0 (xy 평면상)
\( 0 \leq \rho \l a \)에서 (그 외엔 도체 판 위니 퍼텐셜은 0)

이로부터 tangential 방향과 normal 방향 전기장을 구해보면 각각 다음과 같다. (혹시나 해서 말하는데 z=0을 대입하고 퍼텐셜을 미분하면 안된다; 복잡하더라도 퍼텐셜을 미분하고 z=0을 대입해야한다)


마지막 논의이다. rho=a에서 E_tan(rho,0)이 발산하는 걸 볼 수 있다. 그 위치는 hole의 edge로, 2.11 절에서 논의했던 것처럼 매우 sharp한 표면에 전하가 존재하기 때문에 그러하다. Ez(rho,0)의 결과는 맨 처음 0<rho<a에서의 전기장에 대한 조건에서 예상된 바와 동일하게 구해졌다. (Ez는 Ez^(1)과 다르다는 것을 유의할것)
도체 판에 대전된 면전하는 다음과 같이 구하면 된다.

E1=0, 즉 판 밑의 전기장이 0일때의 등전위면은 다음과 같이 생겼다. hole의 반지름의 2~3배만 멀어져도 거의 관찰되지 않는다. 쌍극자의 전기장은 점전하보다 더 빨리 감소한다는 것과도 일치.

사실, 원통좌표계에서 elliptic coordinate에서 라플라스 방정식을 풀면 mixed boundary condition 하에서 풀 필요가 없다고 한다. 궁금하다면 3.13절 마지막 문단에 있는 레퍼런스 참고.
이로써 3장을 마친다.
'전자기학' 카테고리의 다른 글
| [잭슨 전자기학] Ch 4.2 (0) | 2024.10.11 |
|---|---|
| [잭슨 전자기학] Ch 4.1 (0) | 2024.10.11 |
| [잭슨 전자기학] Ch3 - (3/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch3 - (2/4) (0) | 2024.10.02 |
| [잭슨 전자기학] Ch3 - (1/4) (0) | 2024.10.01 |